Основные задачи теории информации

ГЛАВА 9. Основные задачи теории информации

         Теория информации - область, в которой изучаются основные количественные закономерности, связанные с получением, хранением, передачей и обработкой информации.

         Теория информации позволяет сравнивать различные системы связи. Решение указанных задач стало возможным лишь с введением в ней таких понятий как энтропия и количество информации, которые позволили получить количественное описание процессов передачи информации и установить их общие закономерности.

         Особенностью теории информации является то, что она изучает предельные возможности статистического и помехоустойчивого кодирования, которые понимаются в том смысле, что допускается любая, в пределе бесконечно большая, продолжительность операций кодирования и декодирования, а также любая сложность кодеров и декодеров.

9.1. Количество информации в дискретных сообщениях. Энтропия источника дискретных сообщений.

Для сравнения различных систем связи необходимо ввести некоторую количественную меру, позволяющую оценивать объем информации, содержащейся в сообщении, и объем передаваемой информации.

         Рассмотрим сначала основные положения теории информации для дискретных систем связи. Обозначим возможные различные символы на входе некоторого блока СПИ через α_i, i = 1,…, m, а выходные символы через y_j, j = 1,…,n. Под символом α_i можно подразумевать символы источника, информационные последовательности, сигналы на входе линии связи, а под символами y_j - символы закодированных сообщений, кодовые последовательности, сигналы на выходе линии связи.

         Рассмотрим простейший случай, когда α_i, i = 1,…, m, взаимно независимые. При этом источник А полностью описывается априорными вероятностями  которые и характеризуют первоначальное незнание (первоначальную неопределенность) о появлении конкретного символа α_i на входе блока.

         При наличии помех между символами α_i и y_j нет однозначного соответствия, т.е. символ α_i может перейти в любой символ y_j с некоторой условной вероятностью которую можно вычислить, если известен механизм такого перехода. Зная вероятности  и  нетрудно найти вероятности  появления на входе блока символов α_i, i = 1,…, m, при условии, что на выходе блока наблюдался символ y_j. Эти вероятности, называемые апостериорными, характеризуют оставшееся незнание (оставшуюся неопределенность) о появлении на входе символов α_i, i = 1,…, m, при наблюдении символа y_j на выходе блока.

Рекомендуемые материалы

         Таким образом, полученная информация о символе α_i при наблюдении символа y_j приводит к изменению вероятности появления символа α_i от ее априорного значения  к ее апостериорному значению . При этом представляется обоснованным взять за количество информации о символе α_i, содержащейся в символе y_j, некоторую функцию только вероятностей  и :

                        (9.1)

Такое определение количества информации, несвязанное с физической природой сообщения, позволяет строить довольно общую теорию, в частности, сравнивать различные системы связи по эффективности.

         В качестве функции  удобно использовать логарифм отношения апостериорной  вероятности к априорной , т.е. определить  как

                              (9.2)

При таком задании, в частности, количество информации обладает свойством аддитивности: количество информации о символе α_i(в дальнейшем для общности рассуждения - событии α_i), доставляемой двумя независимыми символами (событиями) y_j и z_k:

                    (9.3)

Это свойство хорошо согласуется с "интуитивным" понятием информации.

         Основание логарифма может быть любым. От него зависит единица измерения количества информации. В технических приложениях обычно используют основание 2. При этом количество информации I измеряется в двоичных единицах или битах. При проведении математических выкладок зачастую удобно пользоваться натуральными логарифмами. Соответственно информация измеряется в натуральных единицах или натах.

         Введенная величина  обладает важным свойством симметрии по отношению к α_i и y_j:

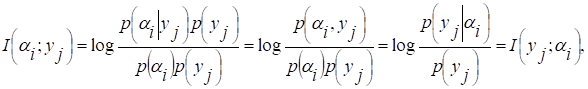
(9.4)

т.е. информация, доставляемая событием y_j о событии α_i равна информации, доставляемой событием α_i о событии y_j. По этой причине  называется взаимной информацией двух случайных событий относительно друг друга.

         Из (9.4) следует, что если события α_i и y_j статистически независимы, то , т.е. независимые события не несут друг о друге никакой информации.

         Взаимная информация при фиксированной вероятности принимает максимальное значение, когда апостериорная вероятность , т.е. когда наблюдаемое событие y_j однозначно определяет событие α_i. При этом

                            (9.5)

         Величина   называется собственной информацией события α_i. Ее можно интерпретировать как количество информации, которое доставляет событие α_i или любое другое, однозначно связанное с ним. Собственная информация всегда является неотрицательной величиной, причем чем менее вероятно событие, тем она больше. Взаимная информация может быть как положительной, так и отрицательной величиной.

         Пусть α_i, y_j, z_k - статистически зависимых события. Предположим, что событие z_k известно. Количество информации о событии α_i, доставляемое событием y_j при условии, что z_k известно, называется условной взаимной информацией. Она определяется так же, как и взаимная информация, однако априорная и апостериорная вероятности должны быть взяты при условии z_k, т.е.

                        (9.6)

Отсюда следует, что условная взаимная информация при фиксированной вероятности  принимает максимальное значение, когда . При этом

                  (9.7)

Величина  называется условной собственной информацией. Ее можно интерпретировать как количество информации, доставляемое событием α_i при известном событии z_k, или как количество информации, которое должно доставляться некоторым другим событием для однозначного определения события при известном z_k.

         Покажем, что взаимная информация удовлетворяет свойству аддитивности. Пусть α_i, y_j и z_k - три статистически зависимых события. Тогда количество информации о событии α_i, которое доставляют события y_j и z_k

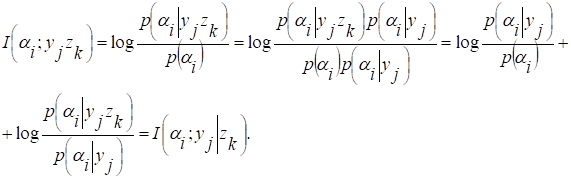
(9.8)

         Таким образом, количество информации о событии α_i, которое доставляют события y_j и z_k, равно сумме информации, доставляемой z_k при известном событии y_j.

         Аналогично можно показать, что

                     (9.9)

         Используя соотношения (9.2), (9.4), (9.5) и (9.7), можно взаимную информацию записать в одной из следующих форм:

                        (9.10)

                          (9.11)

                     (9.12)

где  - собственная информация сложного события α_iy_j.

         Соотношение (9.10) можно интерпретировать следующим образом. Взаимная информация  равна разности между количеством информации, требуемой для определения α_i до и после того, как становится известным y_j. Нетрудно пояснить и соотношения (9.11) и (9.12), а количество информации о множестве А передаваемых символов, которое в среднем содержится в множестве Y принимаемых символов.

.   (9.13)

Величина I(A;Y) называется средней взаимной информацией.

         Нетрудно показать, что

         (9.14)

         На практике также вызывает интерес не собственная информация, а средняя собственная информация.

         (9.15)

Она характеризует количество информации, которое в среднем необходимо для определения любого символа из множества А возможных передаваемых символов.

         Выражение (9.15) идентично выражению для энтропии системы в статистической механике. Поэтому величину I(A) называют энтропией дискретного источника А и обозначают через Н(А). Чем больше Н(А), тем более неопределенным является ожидаемый символ. Поэтому энтропию можно рассматривать как меру неопределенности символа до того, как он был принят.

         Из (9.15) следует, что Н(А)≥0, т.е. энтропия является неотрицательной величиной. Она обращается в нуль, когда одна из вероятностей р(α_i) равна единице, а остальные нулю. Этот результат хорошо согласуется с физическим смыслом. Действительно, такая ситуация возникает, например, когда передается только один символ. Поскольку он заранее известен, то неопределенность источника равна нулю и с появлением символа мы не получаем никакой информации.

         Энтропия удовлетворяет неравенству

                                           (9.16)

причем знак неравенства имеет место, когда где m - число возможных событий α_i (число различных символов, сообщений и т.п.). Это свойство можно доказать, используя неравенство

                                             (9.17)

Рассмотрим разность

       (9.18)

Учитывая (9.17), находим

   (9.19)

Знак равенства имеет место, когда так как только при  неравенство (9.17) превращается в равенство. При этом энтропия принимает максимальное значение .

         Из (9.16) вытекает следующий важный вывод: при заданном алфавите символов количество информации, которое в среднем может содержаться в одном символе, достигает максимума, когда все символы используются с равной вероятностью. При этом величину  называют информационной емкостью алфавита.

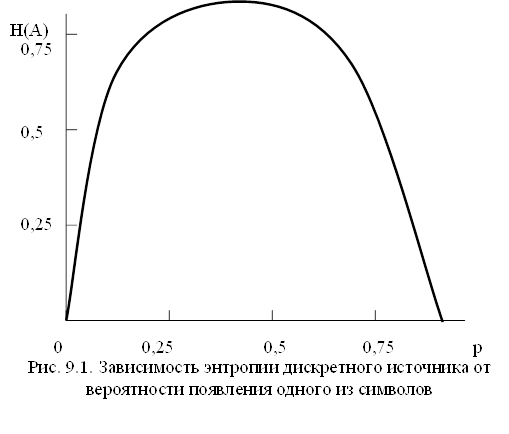
         Для алфавита, состоящего из двух символов,

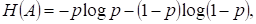
где р - вероятность появления одного из символов. При р = 1/2 (рис.9.1.) энтропия принимает максимальное значение дв.ед. Таким образом, двоичная единица информации, или бит, - количество информации, которое содержится в одном двоичном символе, появляющемся с вероятностью р=0,5.

Подобно тому, как было введено понятие средней собственной информации, можно ввести понятие условной собственной информации:

   (9.20)

         Величина  характеризует количество информации, которое в среднем необходимо для определения любого символа из алфавита А при известном множестве событий Z, т.е. характеризует неопределенность символа алфавита А до того, как он был принят, при условии, что множество событий Z известно. Она называется условной энтропией и обозначается через .

         Используя неравенство (9.17), нетрудно показать, что

                                    (9.21)

причем знак равенства имеет место, когда события α_i и z_k статистически независимы ( для всех индексов i и k).

         Соотношение (9.21) играет важную роль в теории кодирования. На его основе можно сделать следующий вывод: для того, чтобы каждый символ кодовой комбинации доставлял как можно больше информации, необходимо обеспечивать статистическую независимость каждого символа кодовой комбинации от предыдущих символов.

         Можно ввести понятие энтропии множества совместных событий A и Z:

    (9.22)

Подставляя вместо вероятности  под знаком логарифма произведение , выражение (9.22) можно привести к виду

                            (9.23)

Если события α_i и z_k статистически независимы, то формулу (9.23) можно переписать в виде

                              (9.24)

         Соотношения (9.23) и (9.24) есть не что иное, как свойство аддитивности энтропии.

         Среднюю взаимную информацию можно представить как

                            (9.25)

                             (9.26)

                  (9.27)

         Выражение (9.25) имеет простую физическую интерпретацию, когда  α_i- переданный символ, а  y_j - принятый. При этом Н(А) можно рассматривать как среднее количество передаваемой информации, H(A│Y) - как среднее количество информации, теряемой в канале связи (величину H(A│Y) обычно называют надежностью), I(A;Y) - как среднее количество информации, получаемой с приходом каждого символа. Нетрудно дать соответствующие интерпретации соотношениям (9.26) и (9.27).

         Энтропия H(Y│A)  определяется только помехой в канале связи и называется шумовой.

         Пусть  T_C   - среднее время передачи одного символа. Тогда величина R=I^′(А;Y)=(1/ T_C ) I(A;Y) характеризует среднее количество информации, передаваемое в единицу времени. Ее называют скоростью передачи информации.

         Величина H`(A)=(1/T_c)H(A) характеризует среднее количество информации, выдаваемое источником. Ее называют производительностью источника.

         Найдем среднее количество информации, передаваемое по двоичному симметричному каналу (рис.9.2)

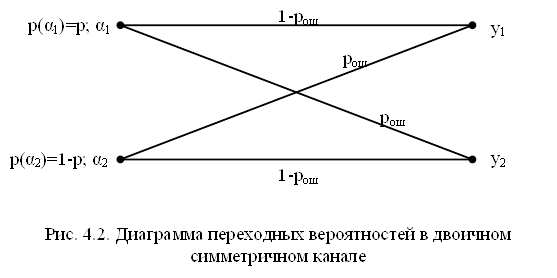
Пусть на вход канала поступают двоичные символы α₁ и α₂ с вероятностями р и (1-р) соответственно. На выходе канала появляются двоичные символы y₁ и y₂. Вероятность ошибки при передаче любого символа равна р_ош. Таким образом,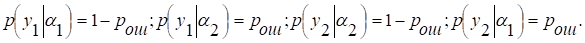

         Воспользуемся формулой (9.26). Энтропия

.

С учетом рассматриваемой модели канала

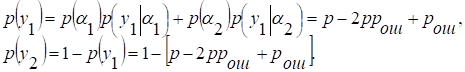
Нетрудно убедиться, что H(Y) принимает максимальное значение, равное 1, при р = 1/2.

         Условная энтропия

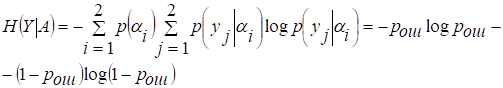
Заметим, что для рассматриваемого случая H(Y│A) не зависит от вероятности р.

         Подставляя выражения для H(Y) и H(Y│A) в (4.21), находим I(A;Y). В частности, при р = 1/2

       (9.28)

Таким образом, среднее количество информации, передаваемое каждым символом по двоичному симметричному каналу, при р = 1/2 зависит только от вероятности ошибочного приема символа (рис. 9.3)

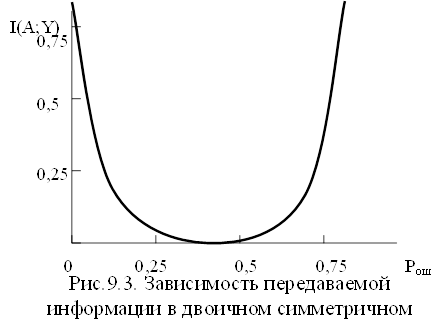
В отсутствие помех (р_ош=0) I(A;Y)=1 дв.ед., при р_ош=1/2 I(A;Y)=0, т.е. никакой информации не передается; при р_ош=1 I(A;Y)=1 дв.ед. В последнем случае, хотя все принятые символы ошибочные, однако передаваемые сообщения можно легко восстановить, поставив в соответствие сигналу  y₁ символ α₂, а сигналу y₂ символ α₁.

9.2. Избыточность сообщений

         Рассмотрим ансамбль A, состоящий из m различных символов . Энтропия такого дискретного источника достигает максимального значения , когда символы статистически независимы и появляются на его выходе с одинаковой вероятностью, равной 1/ m. На практике часто символы неравновероятны и зависимы. Поэтому энтропия источника . Соответственно количество информации, доставляемое такими символами, меньше возможного в  раз.

         Пусть сообщение состоит из n символов. Очевидно, что количество информации в нем . При использовании алфавита с максимальной энтропией для передачи такого же объема информации потребовалось бы число символов. Очевидно, что количество информации в нем I=nH(A). При использовании алфавита с максимальной энтропией для передачи такого же объема информации потребовалось бы число символов

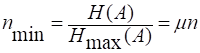
где, - коэффициент, характеризующий допустимую степень сжатия сообщений.

         Величина  называется избыточностью источника.

9.3. Пропускная способность дискретных каналов с шумом

Среднее количество информации, передаваемое по дискретному каналу в расчете на один символ, определяется как

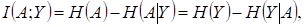
где А и Y -множества символов на входе и выходе канала. Энтропия Н(А) определяется только источником входных символов. Энтропии H(A│Y), H(A) и H(Y│A) в общем случае зависят как от источника входных символов, так и от свойств канала. Поэтому скорость передачи информации зависит не только от канала, но и от источника сообщений. Максимальное количество переданной информации в единицу времени, взятое по всевозможным источникам входных символов (по всем многомерным распределениям вероятности Р(А), характеризующим эти источники),

                                   (9.29)

называется пропускной способностью канала.

         Пропускную способность канала можно определить и в расчете на символ:

                               (9.30)

9.4. Пропускная способность непрерывных каналов с

аддитивным шумом

Пусть сигнал y(t) на выходе канала представляет собой сумму полезного сигнала x(t) и шума n(t), т.е.

y(t) = x(t) + n(t), 0≤t≤T,                           (9.31)

причем сигнал x(t) и шум n(t) статистически независимы. Допустим, что канал имеет ограниченную полосу пропускания шириной F_к. Тогда в соответствии с теоремой Котельникова функции y(t) , x(t) и n(t) можно представить совокупностями отсчетов y_i, x_i и n_i, i=1,…,M, где М = 2F_кТ. При этом статистические свойства сигнала x(t) можно описать многомерной плотностью вероятности  а статистические свойства шума - плотностью вероятности   где x и n - векторы с координатами  и  соответственно.

         Пропускная способность непрерывного канала

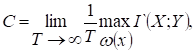
где - количество информации о какой-либо реализации сигнала x(t) длительности Т, которое в среднем содержит реализация сигнала y(t) той же длительности Т, максимум ищется по всем возможным распределениям ω(x).

         Среднюю взаимную информацию можно определить как

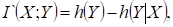
где

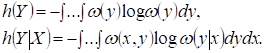
Заметим, что с учетом (9.31) условная плотность вероятности  и

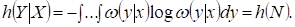
         Таким образом, пропускная способность непрерывного канала с аддитивным шумом

                          (9.32)

         Вычислим пропускную способность непрерывного канала без памяти с аддитивным белым гауссовским шумом, имеющим одностороннюю спектральную плотность N₀, для случая, когда средняя мощность полезного сигнала равна P_c. При этом отсчеты шума оказываются статистически независимыми и дифференциальная энтропия

  (9.33)

где  - дисперсия шума n(t).

         Определим максимально возможное значение дифференциальной энтропии h(Y). Прежде всего отметим, что

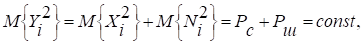
т.е. средний квадрат отсчета Y_i фиксирован. При этом дифференциальная энтропия h(Y_i) принимает максимальное значение, когда случайная величина Y_i  является гауссовской с нулевым математическим ожиданием. Это имеет место, если случайная величина X_i гауссовская с нулевым математическим ожиданием.

         Дифференциальная энтропия h(Y) совокупности из n отсчетов будет максимальна, если отсчеты будут статистически независимы. Это имеет место, если спектральная плотность мощности процесса X(t) равномерна в полосе частот F_k.

         При выполнении указанных требований к сигналу

                          (9.34)

         Подставляя (9.33) и (9.34) в (9.32), находим

                    (9.35)

         Формулу (9.35) часто называют формулой Шеннона. Подчеркнем, что она справедлива для следующей идеализированной модели канала связи. Выходное колебание y(t) представляет собой сумму входного сигнала x(t) и шума n(t), причем сигнал и шум являются статистически независимыми гауссовскими случайными процессами с нулевыми математическими ожиданиями и имеют равномерные спектральные плотности мощности в полосе частот .

         Формула (9.35) очень важна для системы связи, так как она устанавливает связь между пропускной способностью непрерывного канала с ограниченной полосой частот и техническими характеристиками системы: шириной полосы пропускания канала и отношением сигнал/шум. Из нее следует, что одну и ту же пропускную способность можно получить при различных соотношениях F_k и P_c/P_ш. Другими словами, формула (9.35) указывает на возможность обмена полосы пропускания на мощность сигнала и наоборот. С учетом зависимостей С от F_k и С от P_c/P_ш очевидна целесообразность обмена мощности сигнала на полосу.

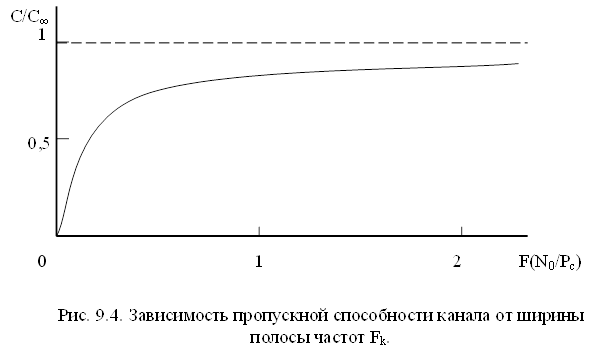
         Из (9.35) нетрудно видеть, что пропускная способность канала растет с увеличением полосы частот F_k (рис.9.4.) и при  стремится к предельному значению

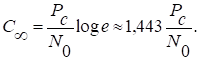
Вам также может быть полезна лекция "21 Система премирования работников".

Заметим, что пропускная способность непрерывного канала, в котором действует шум, отличный от белого гауссовского, больше, чем дает формула (9.35)

9.5. Теорема кодирования для канала с помехами

         Пропускная способность дискретного и непрерывного каналов характеризуют их предельные возможности как средств передачи информации. Они раскрываются в фундаментальной теореме теории информации, которая известна как основная теорема кодирования К.Шеннона. Применительно к дискретному источнику она гласит: если производительность источника сообщений H^{`</sup>(A)  меньше пропускной способности канала С, то существует по крайней мере одна процедура кодирования и декодирования, и ненадежность H(A│Y) могут быть сколь угодно малы. Если H<sup>`}(A)>C, то такой процедуры не существует.

         Результат основной теоремы кодирования для канала с шумом в определенной степени неожидан. В самом деле, на первый взгляд кажется, что уменьшение вероятности ошибок в передаче сообщений требует соответствующего уменьшения скорости передачи и, что последняя должна стремиться к нулю вместе с вероятностью ошибок. Такой вывод, в частности, вытекает из рассмотрения многократной повторной передачи символов источника по каналу как способа уменьшения вероятности ошибок в передаче сообщений. В этом случае при наличии помех в канале связи обеспечить стремление к нулю вероятности ошибки в передаче сообщения можно только при стремлении скорости передачи к нулю.

         Однако теорема кодирования показывает, что в принципе можно вести передачу со скоростью, сколь угодно близкой к С, достигая при этом сколь угодно малой вероятности ошибки. К сожалению, теорема, указывая на принципиальное существование помехоустойчивого кода, не дает рецепта его нахождения. Можно лишь отметить, что для этого необходимо применять коды большой длины. При этом по мере приближения скорости передачи к пропускной способности и уменьшения вероятности ошибки код усложняется вследствие увеличения длины блоков, что приводит к резкому усложнению кодирующего и декодирующего устройств и запаздыванию при декодировании. Применяемые в настоящее время способы кодирования не реализуют потенциальных возможностей систем связи. О степени совершенства системы связи можно судить по отношению .

         Для канала с пропускной способностью С, на входе которого включен источник непрерывных сообщений, К.Шеннон доказал следующую теорему: если при заданном критерии эквивалентности сообщений источника  его эпсилон-энтропия  меньше пропускной способности канала С, то существует способ кодирования и декодирования, при котором погрешность воспроизведения сколь угодно близка к . При  такого способа не существует.