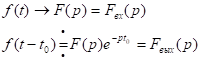Операторный метод расчёта переходных процессов
Лекция№4
Операторный метод расчёта переходных процессов.
Основан на преобразовании Лапласа.
 функция комплексной переменной p
функция комплексной переменной p
 оригинал,
оригинал,  -изображение.
-изображение.
 - прямое преобразование Лапласа.
- прямое преобразование Лапласа.
 -обратное преобразование Лапласа
-обратное преобразование Лапласа
И прямое и обратное преобразование это некоторый определенный интеграл.
Свойства преобразования Лапласа:
Рекомендуемые материалы
1)  2)
2) 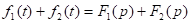
3)  4)
4) 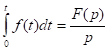
Последние 2-а свойства наиболее важны, т.к. производная и интеграл выражаются через изображение самой функции. Если применить преобразование Лапласа к СДУ, то получится система алгебраических уравнений относительно изображений переменных. Из полученной системы алгебраических уравнений можно найти изображения переменных, а потом через обратные преобразования найти оригинал.
Изображения некоторых функций
 1.
1.
Это изображение постоянной величины после коммутации
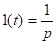
2. 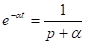
3.  функция Дирак
функция Дирак
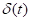


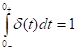
 Функцию Дирака можно представить в виде последовательности следующих функций:
Функцию Дирака можно представить в виде последовательности следующих функций:
Переход от изображения к оригиналу обычно сводится к тому, что изображение искомой величины преобразуется к табличному виду.
Решение системы алгебраических уравнений как известно даёт выражение в виде дробно-рациональной функции.

 многочлены
многочлены
Если многочлены представляют собой правильную дробь, то она (функция) может быть разложена на элементарные дроби:
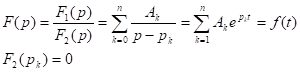
Рассмотрим способ разложения на элементарные дроби.
 умножим обе части на
умножим обе части на  и вычислим предел
и вычислим предел
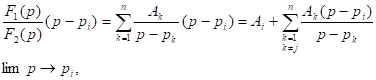
тогда
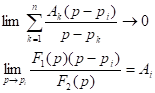
(найдем предел по правилу Лопиталя)
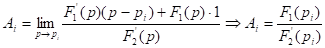
Корни могут быть и комплексные: если корни комплексные, то они образуют комплексно сопряжённые пары:

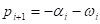
Тогда  тоже будет комплексным:
тоже будет комплексным:
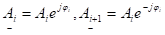
Найдём оригинал от этих двух слагаемых:

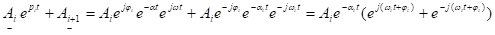
(поделим и умножим на 2), получим
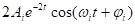
Если корни комплексные, то нужно найти  для того корня, у которого мнимая часть положительная, а затем записать оригинал для двух слагаемых.
для того корня, у которого мнимая часть положительная, а затем записать оригинал для двух слагаемых.
В теории цепей обычно вместо того, чтобы применять преобразования Лапласа к ДСУ используют операторные схемы.
 Операторные схемы: 1)
Операторные схемы: 1)

применим преобразование Лапласа К этому уравнению
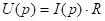

-закон Ома справедлив для изобр-ий.
2) 
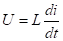
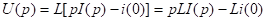
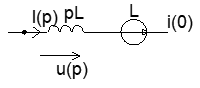
3) 
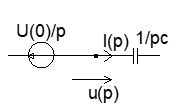
 применим преобразование Л.
применим преобразование Л.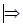
Порядок расчёта:
1. Из режима до коммутации найти токи в индуктивности и напряжения в ёмкостях.

2. Составляем операторную схему.
3. Ищем необходимые изображения токов и напряжений из операторной схемы: 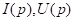
4. От изображений переходим к оригиналам

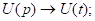
Пр.: E = 10 B; L = 1 мГн
 С = 1 мкФ;
С = 1 мкФ;  Ом
Ом
 Ом
Ом
 1.
1. 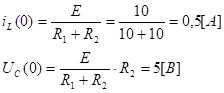
 2.
2.
3.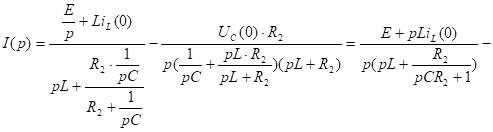
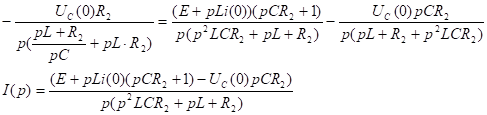
4. 


1) 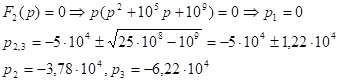
2) 
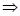
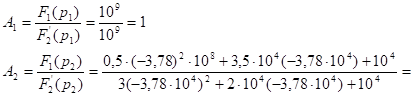
Ответ: 
В настоящее время операторный метод – основной метод анализа цепей.
Переходная и импульсная характеристика цепей.
В частотной области использовались понятия АЧХ и ФЧХ, Когда анализируем свойства цепей в переменной области используются переходные и импульсные характеристики.
Опр: Переходной характеристикой цепи называется отношение реакции цепи к волне скачкообразного воздействия на входе при нулевых независимых начальных условиях.
 -входная волна – напряжение
-входная волна – напряжение

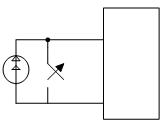
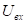
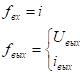
 переходная характеристика
переходная характеристика
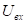

Переходная характеристика цепи численно равна
реакции цепи на единичную функцию
(единичный скачок тока или напряжения).
Экспериментальное определение переходной характеристики:
В соответствии с определением нужно поставить ключ и зафиксировать на осциллографе какую-то волну. Нужен запоминающий осциллограф, который позволяет просматривать единичную волну. Такие осциллографы существуют, но они дороже, чем обычные для периодических сигналов.

ГПИ – генератор переменных импульсов
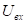
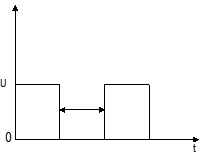
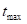
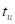
Длительность импульса должна быть такой, чтобы переходной процесс закончился:
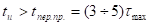
Длительность паузы должна быть такой, чтобы исследуемая цепь успела вернуться к нулевым начальным условиям:
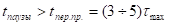
Лекция № 5
 Порядок расчёта:
Порядок расчёта:
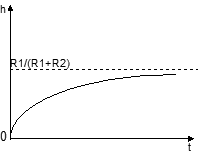
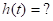
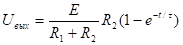

Пр.2:

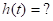
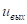
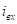
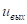
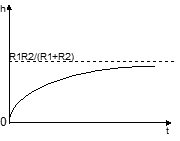
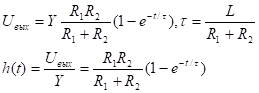
Импульсная характеристика цепи.
Импульсной характеристикой цепи называется отношение выходной величины к площади импульсного входного воздействия, при перпендикулярных начальных условиях равных 0.

 - импульсная характеристика цепи.
- импульсная характеристика цепи.
Выходная величина – это либо ток, либо напряжение.
 - если напряжение, то [B·C], ток – [A·C].
- если напряжение, то [B·C], ток – [A·C].
Воздействие считается импульсным, если его длительность <<характерного времени реакции цепи.
Идеальный импульс – это дельта-функция.
Он бесконечно короткий и его площадь =1
 - преднулевые
- преднулевые  - нулевые
- нулевые
 - начальные условия
- начальные условия  - начальные условия
- начальные условия
Особенность расчёта импульсной характеристики в том, что здесь нарушаются правила коммутации.
 Измерение импульсной характеристики
Измерение импульсной характеристики

 - длительность импульса
- длительность импульса

Длительность паузы такая, чтобы переходной процесс после прохождения импульса закончился: 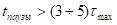
Расчёт импульсной характеристики:
 Удобнее всего вести операторным методом
Удобнее всего вести операторным методом
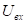
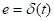
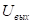
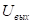
1. Режим до коммутации: 
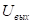
 2.
2.
3. 
4. 
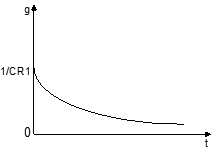
При расчёте импульсных характеристик, изображение выходной величины не всегда бывает правильной дробью, иногда высшая степень числителя равна высшей степени знаменателя. В этом случае для перехода к оригиналу неправильную дробь нужно представить в виде правильной дроби и целой части. При этом импульсная
характеристика в своём составе будет иметь дельта-функцию.
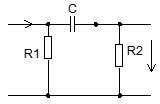
Пр.:
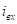
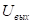
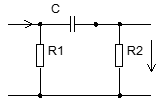 |
g(t)=?
Операторная схема:
 2.
2.
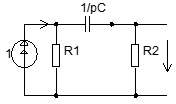
3. 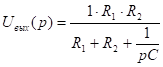
4.  - степень в числителе и знаменателе одинаковы, разделим числитель на знаменатель.
- степень в числителе и знаменателе одинаковы, разделим числитель на знаменатель.
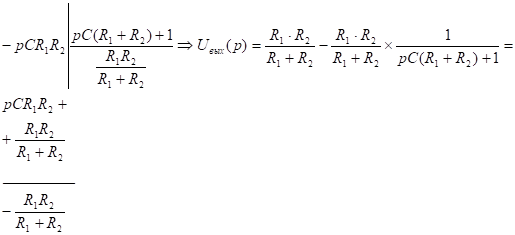
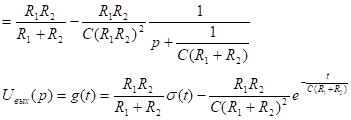
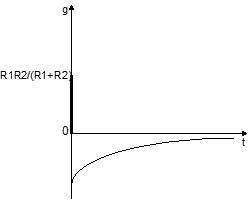
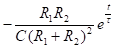
Связь между переходной и импульсной характеристикой
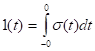
В теории обобщенной функции устанавливается понятие производной для функции, если она имеет скачок. Производная в точке разрыва = величине скачка умноженного на дельта-функцию 
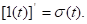
Т.о если воздействие на входе связано между собой через обобщенную производную, то такая же связь будет между реакциями цепи.

Скачок в переходной характеристике может быть только при t = 0
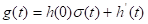
 Пр.:
Пр.:
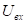

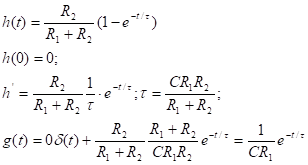
Пр.:
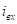
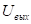
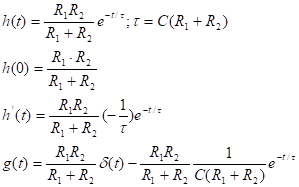
Передаточная функция цепи.
Опр.: Передаточной функцией цепи называется отношение операторного изображения выходной величины к операторному изображению входной величины при преднулевых начальных условиях = 0
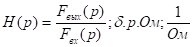
Входная и выходная величина – как ток, так и напряжение.
Связь передаточной функции с другими функциями цепи.

 ;
;
Поскольку передаточная функция не зависит от вида входной величины, то пусть
 тогда:
тогда:
 - оригинал от импульсной характеристики
- оригинал от импульсной характеристики

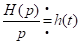
Т.о.: 
 анализ цепи в частотной области
анализ цепи в частотной области

 - во временной области
- во временной области
Пр.: Предположим, что нужно построить запаздывающую цепь

- запаздывание сигнала
В лекции "6 Принцип платности пользования природными ресурсами" также много полезной информации.