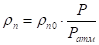Уравнения для расчёта коэффициента теплоотдачи
Уравнения для расчёта коэффициента теплоотдачи
В зависимости от агрегатного состояния, от вида поверхности, от типа конструкции, от режимов течения теплоносителей в общем случае коэффициент теплоотдачи определяется из уравнения Нуссельта, зависящего от ряда факторов:  .
.
Температура стенки является определяющей для теплофизических величин греющего теплоносителя:  ,
,  .
.
Для начала расчёта температурой стенки необходимо задаться, а затем, рассчитав  и
и  , его значение уточнить.
, его значение уточнить.
I. При движении теплоносителя в прямых трубах круглого сечения или в каналах не круглого сечения, без изменения агрегатного состояния.
a) При развитом турбулентном движении.
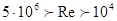
 , (1)
, (1)
Определяющим диаметром является эквивалентный диаметр трубы. 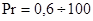
Для изогнутых труб:  , где
, где
Рекомендуемые материалы
 – внутренний диаметр трубы змеевика,
– внутренний диаметр трубы змеевика,
 – диаметр витка змеевика.
– диаметр витка змеевика.
b) Для переходного режима: 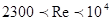
 (2)
(2)
c) Для ламинарного режима: 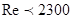
 – вязкостный,
– вязкостный,
Для труб круглого сечения или каналов прямоугольной формы: 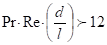
 (3)
(3)
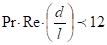
 (4)
(4)
 – вязкостно-гравитационный.
– вязкостно-гравитационный.
 (5).
(5).
II. При движении теплоносителя в межтрубном пространстве 2-х трубного теплообменника.
Расчёты ведутся по формулам (2)-(5). В качестве определяющего размера используется эквивалентный диаметр кольцевого сечения между трубами.
 .
.
Для развитого турбулентного движения расчёт ведётся по выражению:  (6)
(6)
III. При движении теплоносителя в межтрубном пространстве кожухотрубного аппарата с сегментными перегородками.
При  :
:  (7)
(7)
При  :
:  (8)
(8)
При этом скорость потока определяют для наименьшего сечения в межтрубном пространстве.
IV. При обтекании пучка оребрённых труб.
 – диаметр ребра;
– диаметр ребра;
 – наружный диаметр несущей трубы;
– наружный диаметр несущей трубы;
 – высота ребра;
– высота ребра;
 – шаг ребра;
– шаг ребра;
 .
.
 (9)
(9)
Определяющим размером является шаг ребра ( ).
).
Уравнение применимо для чисел Re от 3000 до 25000, при этом  .
.
Полученное в уравнении (9) значение коэффициента теплоотдачи ребра –  подставляется в уравнение для теплопередачи полной поверхности:
подставляется в уравнение для теплопередачи полной поверхности:
 (10), где
(10), где
 – коэффициент теплоотдачи внутри трубы;
– коэффициент теплоотдачи внутри трубы;
 – полная поверхность;
– полная поверхность;
 – внутренняя поверхность несущей трубы.
– внутренняя поверхность несущей трубы.
V. При движении теплоносителя в каналах, образованных гофрированными пластинами в пластинчатых теплообменниках.
a) При развитом турбулентном движении
 , (11)
, (11)
· Для пластин 0,2К, S=0,2м2
а=0,086; b=0,73;
 ,
,  .
.
· Для пластин типа 0,3м2
а=0,1; b=0,73;
 ,
,  .
.
· Для пластин 0,5м2 типа 0,5Е – пластины в ёлочку.
а=0,135; b=0,73;
 ,
,  .
.
· Для пластин 0,5м2 типа 0,5Г – горизонтальные гофры.
а=0,165; b=0,65;
·  ,
,  .
.
11. При ламинарном режиме движения.
 (12)
(12)
| Тип поверхности | а | Re не менее | Pr не более |
| 0,2К 0,3 (м2) 0,5Е 0,5Г | 0,5 0,6 0,63 0,46 | 100 100 100 200 | 20 50 80 50 |
VI. Для жидкостей перемешиваемых в аппарате мешалкой.
 (13)
(13)
 , где
, где
 – внутренний диаметр аппарата;
– внутренний диаметр аппарата;
 , где
, где
 – число оборотов мешалки в секунду;
– число оборотов мешалки в секунду;
 – диаметр окружности описанной мешалкой.,
– диаметр окружности описанной мешалкой.,
· При передаче теплоты через рубашку:
 ,
,  ;
;
· При передаче теплоты змеевиковой поверхности:
 ,
,  .
.
VII. При плёночной конденсации насыщенного пара и ламинарном стекании плёнки конденсата под действием силы тяжести.
 (14)
(14)
· Для вертикальной поверхности:
 ,
,  ,
,  – разность температуры конденсата и температуры стенки со стороны греющего теплоносителя (
– разность температуры конденсата и температуры стенки со стороны греющего теплоносителя ( );
);
· Для одиночной горизонтальной трубы:
 ,
,  ,
,  – разность температуры конденсата и температуры стенки со стороны греющего теплоносителя (
– разность температуры конденсата и температуры стенки со стороны греющего теплоносителя ( );
);  – удельная теплота конденсации, определяемая по температуре конденсата на линии насыщения для воды и водяного пара.
– удельная теплота конденсации, определяемая по температуре конденсата на линии насыщения для воды и водяного пара.
Физические характеристики конденсата определяются по средней температуре плёнки конденсата, а именно:
 .
.
Когда величина  не превышает
не превышает  , то физические характеристики могут быть определены по температуре конденсации.
, то физические характеристики могут быть определены по температуре конденсации.
При конденсации пара на поверхности пучка труб из n-горизонтальных труб, то средний коэффициент теплоотдачи α меньше, чем в случае с одиночной трубой из-за утолщения плёнки конденсата на трубах.
Для пучка труб нужна поправка:
 (15)
(15)
ε=0,7 – при n 100;
100;
ε=0,6 – при n>100.
При подстановке в формулу (14) величины  :
:
 (16)
(16)
– для вертикальной поверхности:  ,
,  ;
;
– для горизонтальной поверхности:  ,
,  .
.
Зная расход пара  и подставляя в уравнение (14):
и подставляя в уравнение (14):
 .
.
– для n-вертикальных труб:
 (17)
(17)
– для n-горизонтальных труб:
 (18), где
(18), где
 – приведенная длина канала.
– приведенная длина канала.
Если 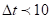
 – расчёт ведётся по формуле (14) – для гофрированных поверхностей приведенная длина канала выбирается по ГОСТ 15518-78.
– расчёт ведётся по формуле (14) – для гофрированных поверхностей приведенная длина канала выбирается по ГОСТ 15518-78.
| 0,2м2 | 0,3 | 0,5 | 0,6 | 1,3 | |
|
| 0,45 | 1,12 | 1,15 | 0,893 | 1,91 |
Если  , то справедлива следующая формула:
, то справедлива следующая формула:
 (19), при этом
(19), при этом
 ,
,  ,
,  , где
, где
F – полная поверхность теплообменника;
G1 – расход пара.
| 0,2м2 | 0,3 | 0,5Е | 0,5Г | |
| a | 338 | 322 | 240 | 376 |
VIII. При пузырьковом кипении.
a) При кипении на поверхностях, погружённых в большой объём.
Лекция "13 Распознавание образов" также может быть Вам полезна.
 (20)
(20)
b) При кипении в трубах.
 (21).
(21).
Критическая удельная тепловая нагрузка, при которой пузырьковое кипение переходит в плёночное, а коэффициент теплоотдачи принимает максимальное значение можно определить формулой при кипении в большом объёме:
 .
.
В формулы (20-22) все физические характеристики жидкости и  подставляются при атмосферном давлении (760 мм рт.ст.), а
подставляются при атмосферном давлении (760 мм рт.ст.), а  берётся при давлении над поверхностью жидкости. По этому же давлению определяется и температура кипения.
берётся при давлении над поверхностью жидкости. По этому же давлению определяется и температура кипения.