Спектр непериодического сигнала конечной длительности
Спектр непериодического сигнала конечной длительности
Из примера спектра периодической последовательности импульсов
видно, что при Т®¥ спектральные линии становятся бесконечно близкими друг к другу и спектр становится сплошным, а форма огибающей спектра сохраняется. Линейчатый спектр заменяется непрерывной комплексной спектральной функцией S(w).
Спектр непериодического сигнала представляет преобразование Фурье:
Если Вам понравилась эта лекция, то понравится и эта - Использование токов высокой частоты.
- обратное преобразование.
Из сопоставления спектральной функции сигнала S(ω) и спектра комплексных амплитуд его периодического продолжения 
следует, что 
т.е. вид функций S(ω) и Cn в общем случае одинаков и отличается только множителем. Соотношение размерности этих функций 
.
Спектральную функцию называют также спектральной плотностью, плотностью амплитуд. Подобно плотности вещества 
- коэффициенту пропорциональности между массой и объемом вещества (объем и масса в пределе стремятся к 0), спектральная плотность – это коэффициент пропорциональности между амплитудой спектральной составляющей в узкой полосе df (ее можно считать одинаковой для всех составляющих в этой полосе) и шириной этой полосы. Физический смысл функции S(ω) - средняя амплитуда, приходящаяся на полосу частот в 1 Гц.
Непериодический сигнал имеет конечную энергию, поэтому его называют «энергетическим». Энергия сигнала
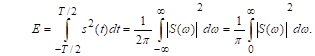
(1)
Проверим соотношение размерностей: 
. Именно такая размерность последнего выражения в формуле (1). Физический смысл функции | S(w)| 2 - спектральная плотность энергии.
