Аэродинамические моменты при отклонении рулевых поверхностей
Лекция 20
Тема 7. Аэродинамические моменты летательного аппарата
7.4. Аэродинамические моменты при отклонении рулевых поверхностей
При рассмотрении темы 3 были рассмотрено разделение рулевых поверхностей на три основных типа:
- несущая поверхность - руль на этой схеме работает при создании управляющих сил и моментов элероны, элевоны, флапероны, рули направления и высоты;
- цельноповоротная несущая поверхность, которая создает управляющие силы и моменты за счет изменения угла между хордой поверхности и соответствующей характерной осью самолета (цельноповоротный стабилизатор, киль и крыло);
- управляющее воздействие достигается изменением структуры потока ( интерцепторы, спойлеры, тормозные щитки, гасители подъемной силы и др.).
Принципы их работы рулевых поверхностей были подробно изложены и зучены в теме 3.
Рассмотрим на примере отклонения горизонтального оперения, как создается им управляющая сила.
Рекомендуемые материалы
Для управления самолетом в продольном канале используется руль высоты или полностью отклоняемый стабилизатор.
Коэффициент подъемной силы горизонтального оперения с учетом отклонения руля высоты  равен
равен
 , (7.11)
, (7.11)
где  го - фактический угол атаки оперения
го - фактический угол атаки оперения  ,
,
 .
.
Для горизонтального оперения, набранного из симметричных профилей, при  =0 и
=0 и  =0
=0
 (7.12)
(7.12)
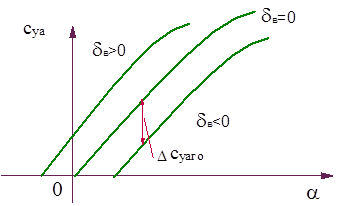
 В силу этого зависимости суаго= f (
В силу этого зависимости суаго= f ( ,
, ) и
) и  для всего самолета с учетом отклонения руля высоты имеет вид, представленный на рисунках.
для всего самолета с учетом отклонения руля высоты имеет вид, представленный на рисунках.
Рис.7.13 Рис.7.14
Аналогичный вид имеет данная зависимость и с учетом отклонения всего стабилизатора
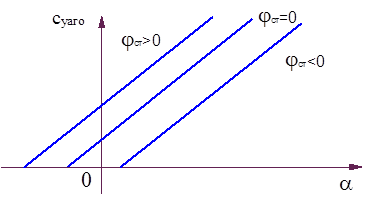 |
Рис.7.15
Таким образом, коэффициент подъемной силы горизонтального оперения с учетом отклонения руля высоты и угла установки стабилизатора определяется выражением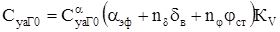
где  - коэффициент эффективности руля высоты,
- коэффициент эффективности руля высоты,
- коэффициент эффективности цельноповоротного стабилизатора.
В прикидочных расчетах можно принимать
 . (7.13)
. (7.13)
Приращение подъемной силы, возникающее на горизонтальном оперении при отклонении руля высоты или цельноповоротного стабилизатора  = вызывает дополнительный момент относительно центра масс
= вызывает дополнительный момент относительно центра масс
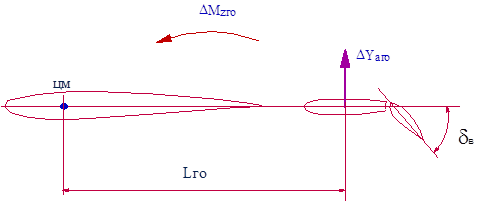
 (7.14) где
(7.14) где 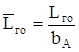
Рис.7.16
Здесь  Суаго представляет собой сумму второго и третьего слагаемых в формуле.
Суаго представляет собой сумму второго и третьего слагаемых в формуле.
В общем случае для самолета
 (7.15)
(7.15)
Тогда зависимость mz=f ( ) при отклонении руля высоты (стабилизатора) смещается вверх или вниз
) при отклонении руля высоты (стабилизатора) смещается вверх или вниз
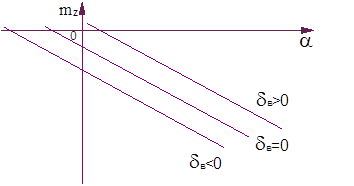 |
Рис.7.17
Шарнирные моменты рулевых поверхностей были подробно рассмотрены в теме 3.
7.5. Аэродинамические характеристики летательного аппарата с учетом балансировки в горизонтальном полете
В установившемся полете самолет должен быть сбалансирован. Под балансировкой понимается уравновешивание сил и моментов, действующих на самолет в полете. Сбалансированный ЛА совершает прямолинейный установившийся полет. Наиболее важной является балансировка ЛА в продольном движении. В этом случае необходимо обеспечит выполнение равенств:
 (7.16)
(7.16)
Продольная балансировка, т.е. обеспечение условия mz=0, осуществляется отклонением руля высоты (стабилизатора)
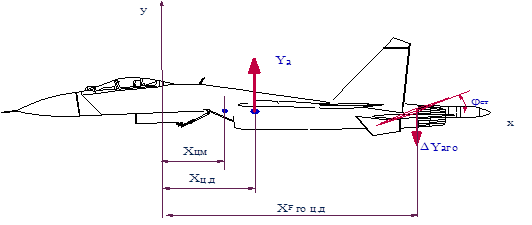
Рис.7.18
Каждому значению угла атаки  и коэффициенту подъемной силы Суа соответствует свой угол поворота стабилизатора (руля высоты) при котором mz=0. Эти значения
и коэффициенту подъемной силы Суа соответствует свой угол поворота стабилизатора (руля высоты) при котором mz=0. Эти значения  и суа называют балансировочными.
и суа называют балансировочными.
Зависимость углов отклонения стабилизатора от суа бал называется балансировочной диаграммой
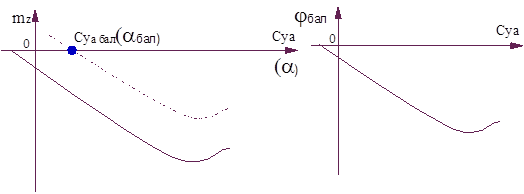 |
Рис.7.19
На ЛА фокус располагается позади центра масс и для того , чтобы сбалансировать ЛА нормальной схемы по моменту тангажа, необходимо на горизонтальном оперении создать дополнительную силу DYго, направленную вниз с тем, чтобы момент этой силы M z р уравновесил момент тангажа M z ЛА. Если фокус ЛА без горизонтального оперения располагается впереди центра масс, то для балансировки по моменту тангажа подъемная сила на оперении направлена вверх; при балансировке она только уменьшается на величину DYго.
7.6.Потери подъемной силы и аэродинамического качества на балансировку и их зависимость от взаимного положения центра масс и аэродинамического фокуса
Для сбалансированного самолета при (mz=0) получаем
 (7.17)
(7.17)
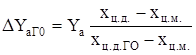
Тогда Yа бал=Yа - D Yа или
 (7.18)
(7.18)
В приближенных расчетах обычно полагают, что фокус и центр давления расположены близко друг от друга и тогда в данных формулах xц.д. заменяют на xF.
Вывод: степень влияния балансировки на величину подъемной силы самолета зависит от расположения горизонтального оперения и запаса продольной статической устойчивости  .
.
 |
Из (7.18) следует, что величина коэффициента подъемной силы при балансировке зависит от разности
 и от расстояния между центром масс самолета и фокусом по отклонению руля, отклоненного для балансировки. На летательном аппарате нормальной схемы и схемы «бесхвостка»
и от расстояния между центром масс самолета и фокусом по отклонению руля, отклоненного для балансировки. На летательном аппарате нормальной схемы и схемы «бесхвостка»  и для них
и для них  . Причем для схемы «бесхвостка» расcтояние от фокуса по отклонению руля (элевона) существенно меньше, чем для нормальной схемы, и поэтому для схемы «бесхвостка» потери подъемной силы на балансировку больше. Для схемы «утка»
. Причем для схемы «бесхвостка» расcтояние от фокуса по отклонению руля (элевона) существенно меньше, чем для нормальной схемы, и поэтому для схемы «бесхвостка» потери подъемной силы на балансировку больше. Для схемы «утка»  и поэтому для нее при при
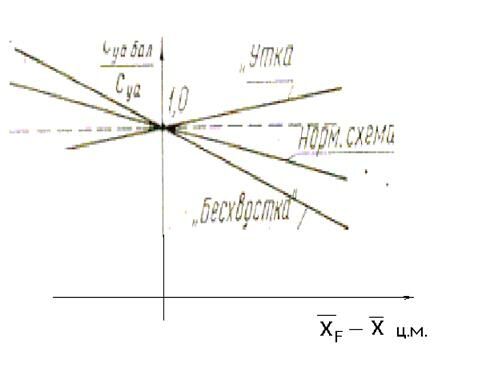
и поэтому для нее при при  при балансировке коэффициент подъемной силы увеличивается. На рис. 7.20 показана зависимость величины отношения
при балансировке коэффициент подъемной силы увеличивается. На рис. 7.20 показана зависимость величины отношения  от разности для указанных трех схем самолетов.
от разности для указанных трех схем самолетов. Рис.7.20
При балансировке летательного аппарата изменяется и величина лобового сопротивления, обусловленного подъемной силой. Дело в том, что при балансировке изменяется величина подъемной силы и для сохранения первого равенства из (7.16) необходимо изменять угол атаки: на летательных аппаратах нормальной схемы и схемы «бесхвостка» увеличивать; схемы «утка»' — уменьшать (при  ). При
). При  направления изменения угла атаки будут обратные. Принято обозначать
направления изменения угла атаки будут обратные. Принято обозначать
 . (7.19)
. (7.19)
Установлено, что для летательных аппаратов с  для схем нормальная и «бесхвостка» kбал> 1 из-за необходимости увеличивать угол атаки. Для схемы «утка» при малых значениях
для схем нормальная и «бесхвостка» kбал> 1 из-за необходимости увеличивать угол атаки. Для схемы «утка» при малых значениях  величина kбал может быть меньше 1,0; при больших значениях
величина kбал может быть меньше 1,0; при больших значениях  . Это связано с тем, что уменьшение сопротивления из-за уменьшения угла атаки (
. Это связано с тем, что уменьшение сопротивления из-за уменьшения угла атаки ( ) не компенсируется его увеличением (
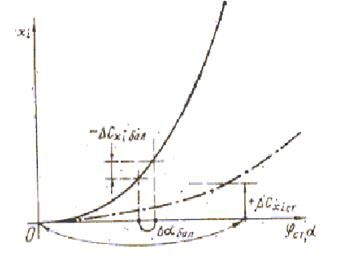
) не компенсируется его увеличением ( ) за счет отклонения на большой угол стабилизатора или руля высоты (рис. 7.21). На летательных аппаратах с
) за счет отклонения на большой угол стабилизатора или руля высоты (рис. 7.21). На летательных аппаратах с  kбал может быть меньше единицы и для схем «нормальная» и «бесхвостка». Качественно зависимости kбал от величины
kбал может быть меньше единицы и для схем «нормальная» и «бесхвостка». Качественно зависимости kбал от величины  для самолетов трех схем могут быть представлены графиком на рис. 7.22.
для самолетов трех схем могут быть представлены графиком на рис. 7.22.
При балансировке изменяется в том числе и максимальное аэродинамическое качество. Если пренебречь несимметрией самолета по подъемной силе, то есть положить aбал =0, то можно записать
 . (7.20)
. (7.20)
 |
В соответствии с (7.19) и рис.7.22 зависимости Кмах бал/Кмах =f(
 ) представлены на рис.7.23.
) представлены на рис.7.23. Лекция 5 - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
Рис.7.21
Вывод: из рис.7.23 следует, что практически для всех схем, за исключением небольшой области для схемы «утка», уменьшение  уменьшает потери аэродинамического качества на балансировку.
уменьшает потери аэродинамического качества на балансировку.
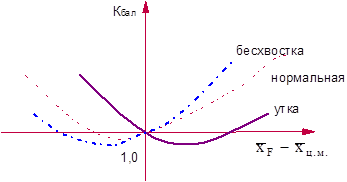 |
Рис.7.22
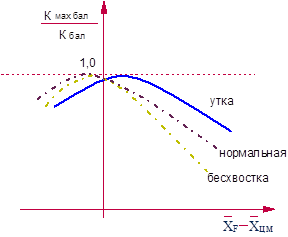 |
Рис.7.23




















