Характеристика жидкости по диаграмме сдвига

Лекция №2.

[dV]= + div(ω)]dV= + ω +div(,ω) + ωdiv=dV+dS=dV+dV=>

=+div-  уравнение Навье-Стокса в векторной форме

=-P

Характеристика жидкости по диаграмме сдвига.

=> =µ  - закон внутреннего трения Ньютона.

m>1 –дилатантные;  m<1- псевдопластичные; m=1 - ньютоновские жидкости.

= =

Рекомендуемые материалы

µ                          ==-кажущийся  коэффициент динамической вязкости.

=+µ- бингамовские жидкости

  Данная система из 5 уравнений в  декартовой системе координат- основное уравнение гидродинамики. Число неизвестных  (ω_x, ω_y, ω_z, ρ_i, P)- 5 равно числу записанных уравнений. Система замкнута. Требуется только запись условий однозначности (краевых условий: начальных и граничных).

Физический смысл: баланс сил- закон сохранения механической энергии системы.

Гидростатика

Система находящаяся в состоянии покоя или равномерного движения является статической, т.е.,,=0

(dx+ dy+dz);

dP=(dx+ dy+dz) –основное уравнение гидростатики.

Изобарическая поверхность- поверхность уровня. Тогда:

dP=0 =>dx+ dy+dz=0 -уравнение поверхности уровня.

Поверхность уровня и давление в сосуде, вращающемся вокруг вертикальной оси.

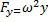
=-g

При вращении образуется параболоид вращения.

+

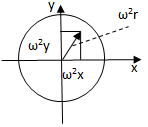
=ρ[dx+ dy+dz]=ρ[+-g]

P-=ρ[g(z-)]- давление в произвольной точке жидкости в сосуде.

Z=+- yравнение  поверхности  уровня

h=+(H-) – закон сохранения объема жидкости

2h=+H

H=+

=h-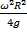

Уравнение поверхности уровня    z=+ h- 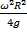- параболоид вращения

Сила давления на боковую стенку сосуда

P=+ρgh – закон Паскаля. Т.к. давление с глубиной погружения меняется, то выделяем бесконечно малый элемент стенки площадью dS, погруженный на глубину h, записываем силу давления на него и интегрируем полученное уравнение:

=PdS=dS+ρg

F=+ρg=( ρg;  - координата центра тяжести стенки, т.к. - статический момент площади dS относительно поверхности уровня.

Гидродинамика

Вывод  выражений для дифференциала Бернулли, интеграла Бернулли (уравнения Бернулли)

Допущения:

1.Течение установившееся

=0

2.Течение осуществляется в поле сил тяжести.

=0, =-g

3.Жидкость является идеальной

= const , µ=0

4.Течение является безвихревым.

ω=0 (ротор вихря)

+=+2 =

Записываем проекции уравнения Навье-Стокса на оси x,y,z, домножаем их соответственно на dx,dy,dz и складываем. Получаем:

½[dx+ dy+ dz]= - 1/ρ[+ + ]-gdz

P=f(x,y,z), тогда имеем полные дифференциалы соответствующих выражений.

 +  + gdz= 0 => d(z+  + )=0,- дифференциал Бернулли.

P, ω, z –давление, скорость, координата в точке – их истинное значение

Z+ += const= H- интеграл (уравнение) Бернулли

 P- среднее давление, ω- средняя скорость, z- координата от живого сечения потока- усредненные параметры.

В идеальных жидкостях  потенциальная энергия + кинетическая энергия неизменны.

Уравнение Бернулли (закон сохранения энергии)

Представление конвективной составляющей вектора скорости в уравнение Навье-Стокса разложением на поступательную и вращательную составляющие (уравнение Громеки-Лэмба)

Докажем, что + =+2

Обратите внимание на лекцию "19 Экзистенциализм".

Выражение для ротора вихря, вращающегося с угловой скоростью ω в декартовой системе

ð 2[ωxω͞  ]_х=-  -  +=+

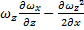
Напомним, что:

=

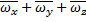
2[ωxω͞  ]= ++- =+,  что и требовалось доказать.