Теория подобия процессов переноса
Лекция 16
Теория подобия процессов переноса.
 =-
=- ; С ростом температуры плотность уменьшается.
; С ростом температуры плотность уменьшается.
 =-
=- ; С ростом
; С ростом 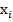 плотность уменьшается (
плотность уменьшается ( - концентрация компонента меньшей плотности).
- концентрация компонента меньшей плотности).
dρ= dt+
dt+ =
= +
+ △t+
△t+ △
△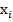 =
= -
- *△t-
*△t- △
△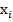
 =P+ρgz – приведенное давление
=P+ρgz – приведенное давление
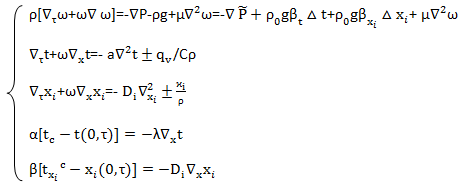
Система уравнений переноса количества движения, тепла и вещества с граничными условиями 3 рода.
Введем безразмерные параметры:
Рекомендуемые материалы
 =
= ;
;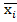 =
= ;
; =
= ;θ=
;θ=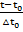
φ= ; Re=
; Re= ; Pe=
; Pe= ;
;  =
=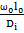
Pr= ;
;  =
= ; Le=
; Le= =
= - критерий Льюиса.
- критерий Льюиса.
 =
= ;
; =
= ;
;
Gr= ;
;  =
= ;
;
 =
= ;
; =
=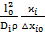
 =
= ; Nu=
; Nu=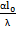
 ω
ω =-∇
=-∇ +
+ θ+
θ+ φ+
φ+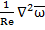
 +Pe
+Pe =-
=-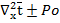
 +
+ =-
=- D
D
Nu[ )]=-∇
)]=-∇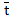
 [
[ )]=-∇
)]=-∇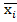
Nu, =f(Fo,
=f(Fo, ,Re,Pr,
,Re,Pr, ,Gr,
,Gr, Po,
Po, ) в случае независимого переноса тепла и вещества имеем:
) в случае независимого переноса тепла и вещества имеем:
Nu= f(Fo, Re, Pr, Gr,
Gr, Po
Po ) ;
) ;  = f(
= f( ,Re,
,Re, ,
, )
)
Аналогия между переносом тепла и массы (аналогия Льюиса)
Для стационарного конвективного переноса тепла и вещества имеем критериальные зависимости:
 =
= =C
=C ;
; =
= = C
= C . Поделим выражения друг на друга:
. Поделим выражения друг на друга:
 =
= =
= =
= =>
=> =
= =
= =
= .
.
Следовательно, зная α, можно рассчитать β и наоборот.
Основное уравнение гидродинамики (Навье-Стокса) для многокомпонентной среды.
В многокомпонентной среде возникает дополнительное изменение количества движения, связанное с диффундирующими потоками массы и источниками (стоками) за счет химического превращения:
 [
[ =
= +
+ dV-
dV- +
+ (
( -
- (
( )]dV
)]dV
Σ =0;
=0; =-
=- и (
и ( +
+ )(
)( -
- )=0
)=0
Σ =0;
=0; =-
=-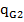
 =
= (
( =
=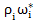
 +
+ =
= (
(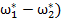
С учетом сделанных замечаний и выполненных ранее преобразований уравнение гидродинамики приводится к виду
ρ[ ω+ω
ω+ω ]=-∇P+ρ
]=-∇P+ρ +∇[µ∇ω-
+∇[µ∇ω- (
(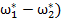 ]
]
Последний член уравнения называют диффузионной вязкостью. Оценим его вклад:
A= =
= =
=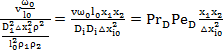
При больших  и малых
и малых  можно пренебречь диффузионной вязкостью.
можно пренебречь диффузионной вязкостью.
Уравнение переноса тепла в многокомпонентной среде
 =ρh; h=Σ
=ρh; h=Σ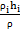
h(t, )=>dh=
)=>dh= dt+Σ
dt+Σ =Cdt+
=Cdt+ d
d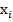
dt= -
- d
d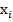 =>
=>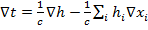
Основное уравнение переноса тепла в многокомпонентной среде:
ρ[ +ω
+ω ]= div q
]= div q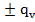
q=-λ∇t+Σ =-λ
=-λ ∇h+
∇h+ Σ
Σ ∇
∇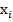 + Σ
+ Σ , т.к. ∇t=
, т.к. ∇t= ∇h
∇h Σ
Σ ∇
∇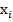
Для примера запишем это уравнение для бинарной среды.
 =1-
=1- ;∇
;∇ ;
; =
=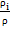
 =
= +
+ =∇
=∇ (
(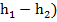
 =
= +
+ =
= (
(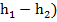 =-ρ
=-ρ ∇
∇ (
(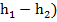 - это частный случай, когда другие коэффициенты переноса равны 0.
- это частный случай, когда другие коэффициенты переноса равны 0.
q=-λ ∇h+
∇h+ (
(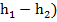 ∇
∇ =-λ
=-λ ∇h+
∇h+ (
(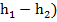 ∇
∇ (1-
(1- )=
)= ∇h+
∇h+ (1-Le) (
(1-Le) (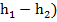 ∇
∇ - последний член- перенос тепла диффузионными потоками.
- последний член- перенос тепла диффузионными потоками.
Информация в лекции "8 Управление издержками обращения в аптеке" поможет Вам.
Уравнение переноса тепла в многокомпонентных системах с учетом выражения для q имеет вид:
ρ[ ]=div[
]=div[ ∇h+
∇h+ (1-Le) (
(1-Le) (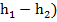 ∇
∇ ]
]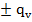
Диффузионным переносом тепла для газов можно пренебречь, ибо Le→1.
Проанализируем, когда можно пренебречь диффузионным переносом тепла.
А= .
.
Это возможно, когда