Комплексный потенциал, комплексная скорость

Комплексный потенциал, комплексная скорость.

Из теории комплексной переменной известно, что если две функции φ и ψ, зависящие от х и у, удовлетворяют условиям Коши-Римана, то комплексная величина будет не просто зависеть, а являться функцией от комплексной переменной , то есть существует некоторая функция , действительной частью которой является φ, а мнимой ψ.  .

Функция  имеет большое значение при изучении плоских потенциальных течений и называется комплексным потенциалом или характеристической функцией течения.

Так как  является аналитической функцией от , то ее производная не зависит от направления дифференцирования, а зависит только от положения точки в пространстве, то есть  

Ещё посмотрите лекцию "8 Политические партии России начала 20 в" по этой теме.

 по условию Коши-Римана:    

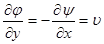
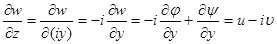
Если вектор U разложить в комплексной плоскости годографа U, то .

Производная от комплексного потенциала дает зеркальное изображение комплексной U относительно действительной оси. Обозначим ее как .

В теории комплексной переменной числа  и  называют сопряженными, назовем  как сопряженную U. Таким образом, производная от комплексного потенциала определяет .

Таким образом, если изменяется какое-то плоское потенциальное течение, то для него можно подобрать уравнение комплексного потенциала, проанализировать его и просчитать составляющие U в любой точке. С другой стороны для любого потенциала можно определить вид течения.