Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме

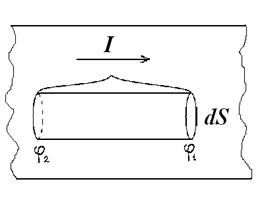
Рассмотрим проводник, в котором течёт ток, и выделим в нём элемент сечением dS и длиной dl.

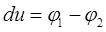
Выведем формулу

,                                                   (1)

где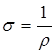

Формула (1) и является законом Ома в дифференциальной форме. Она относится к точке проводника.

– Вывод закона в скалярной форме.

Рекомендуемые материалы

Перейдя к векторной форме, получим формулу (1)

Обратите внимание на лекцию "13 Правление Павла I (1796-1801)".

Задача

Ток течёт по проводнику переменного сечения. Сравните напряжённость поля в области первого и второго сечений. .

Решение , материал – однородный                                                 () ; по формуле (1)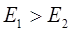

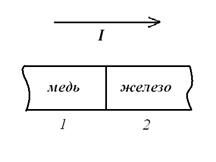
Упражнение:

Проводник составлен из двух материалов: меди и железа () . Сечение постоянно. Найти соотношение напряжённостей  и .