Дифференциальное уравнение равновесия
2.4. Дифференциальное уравнение равновесия жидкости
После рассмотрения некоторых частных случаев равновесия жидкости рассмотрим общее диф
ференциальное равновесия в самом общем виде. Для этой цели выделим отсек жидкости малых размеров в виде параллелепипеда. Масса жидкости в выделенном объёме:
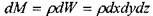
На боковые грани параллелепипеда действуют силы давления: (на левую и правую грани соответственно):
. На переднюю и заднюю грани: 
, на нижнюю
и верхнюю грани: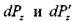
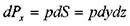
Поскольку давление на правую грань больше, то i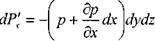
По аналогии можно записать силы давления на остальные пары граней.
на переднюю 
, на заднюю 
, на нижнюю
Рекомендуемые материалы
, на верхнюю
Проекции массовых сил на координатные оси:
на ось ОХ будет на ось ОУ будет
на ось OZ будет
Тогда сумма сил действующих вдоль оси ОХ:
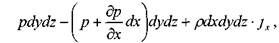
сумма сил действующих вдоль оси 07:
"26 - Артезианские воды" - тут тоже много полезного для Вас.
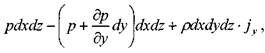
сумма сил действующих вдоль оси OZ:
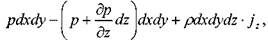
где:
, проекции ускорения массовых сил на координатные оси.
После преобразования получим систему дифференциальных уравнений равновесия жидкости:
i i >
