Лекция 13 - Выбор переменных состояния дискретной системы
Лекция № 13
Тема:
Выбор переменных состояния дискретной системы.
План лекции:
1. Способ прямого программирования.
2. Способ параллельного программирования.
3. Способ последовательного программирования.
1. Способ прямого программирования.
Рассмотрим переход от описания импульсной системы с помощью Z-передаточных функций к описанию с помощью переменных состояния. Как уже отмечалось, выбор переменных состояния не является единственным, и определяется выбором соответствующего базиса. Практически удобным приемом выбора переменных состояния является составление схем моделирования дискретных систем. Схемы включают в себя элементы задержки на такт и сумматоры. Пpи выбope пepeмeнныx cocтoяния импульсных систем за них удобно принимать выходы элементов задержки на такт.
Рекомендуемые материалы
Рассмотрим три способа перехода от Z-передаточной функции дискретной системы к уравнениям (57), (58): способы прямого программирования, последовательного программирования и параллельного программирования на примере звена второго порядка с одним входом и одним выходом и передаточной функцией
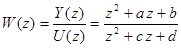
При способе прямого программирования, разделив числитель и знаменатель передаточной функции на 
(в общем случае на 
), получим
(60)
По определению передаточной функции
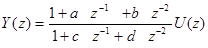
Введем новую переменную e[kT], Z -преобразование которой имеет вид
.
Тогда
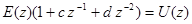
или
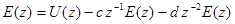
В соответствии с выражением (60) составляем схему моделирования (рис.35). При этом учитываем, что множитель 
соответствует задержке переменной на один такт квантования.
 |
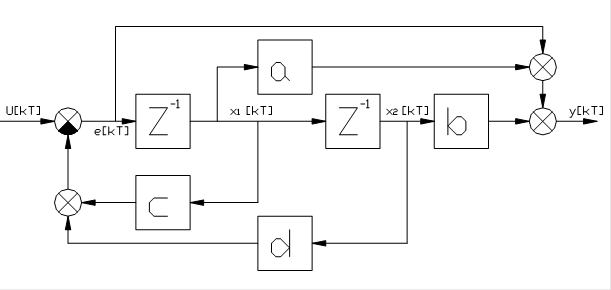Рис. 35
Уравнения состояния системы можно получить, записывая соотношения, связывающие координаты на выходах элементов задержки. В итоге имеем
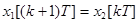
. (61)
Так как
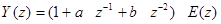
и при этом
,
то для выходной переменной y[kT] получим уравнение
(62)
Таким образом, уравнения (57), (58) принимают вид (61). (62), а матрицы Ф, Н, C, D определяются выражениями
.
Запись системы уравнений (61) для общего случая не представляет сложности. При этом матрица Ф будет иметь структуру, аналогичную собственной матрице системы дифференциальных уравнений, записанных в первой нормальной форме Коши.
2. Способ параллельного программирования.
Рассмотрим способ параллельного программирования. Передаточная функция системы, приведенная к виду (60), разбивается на сумму элементарных звеньев.
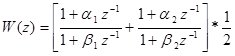
Изображение переменных состояния определяется выражениями
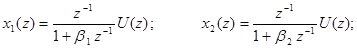
Соответствующая схема моделирования представлена на рис.36.
 |
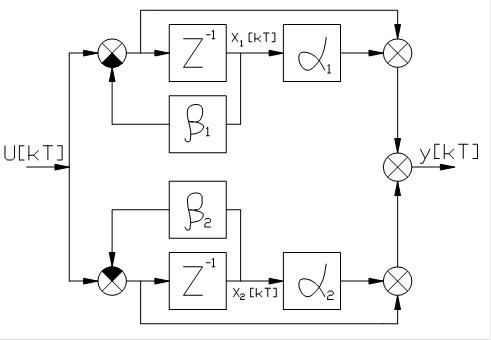Рис.36
Разностные уравнения системы имеют вид
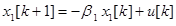
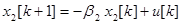
Прежде чем записать уравнение для выходной переменной системы, наполним некоторые преобразования передаточной функции
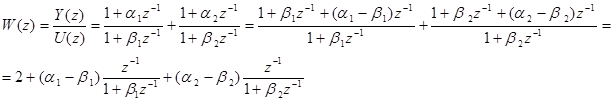
Переходя от изображений к оригиналам, получим
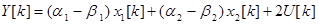
При таком выборе переменных состояния матрицы Ф, Н, С, D соответственно имеют вид
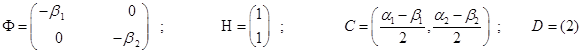
Преимущество этого подхода состоит в том, что собственная матрица дискретной системы Ф оказывается .диагональной, но при этом числа 
(корни характеристического уравнения системы) могут оказаться комплексными. Такие же уравнения можно получить, если передаточную функцию 
непосредственно разложить на простейшие дроби и каждой дроби поставить в соответствие переменную состояния.
3. Способ последовательного программирования.
При использовании способа последовательного программирования уравнению системы в операторной форме придается вид
,
полученный разложением на множители числителя и знаменателя передаточной функции (60). Схема моделирования в этом случае строится в виде последовательности однотипных каскадов (рис.З7)
 |
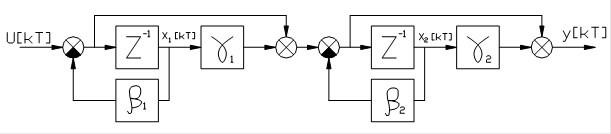Рис.37
Уравнения состояния системы имеют вид
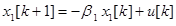
Лекция "Состав и строение соединительной ткани" также может быть Вам полезна.
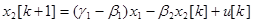
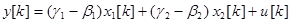
а матрицы Ф, Н, C, D определяются выражением
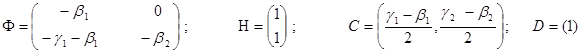
Матрица Ф при этом оказывается треугольной.
Составление блок-схем моделирования дискретных систем является важным этапом их исследования. С помощью этих схем можно рационально выбрать переменные состояния системы, а также перейти к описанию в рамках дискретного преобразования Лапласа или Z-преобразования.
