Отчёт 2
Отчет №2
Оценка характеристик случайного процесса
Дано:
1. Значения содержание кремния в чугуне Si(i).
2. Формула расчета среднего уровня
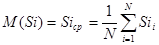
3. Формула расчета дисперсии
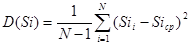
4. Формула расчета среднего квадратического отклонения
Рекомендуемые материалы
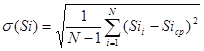
5. Формула расчета автокорреляции случайных процессов
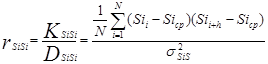
Требуется: Оценить характеристики случайных процессов при N=23
Решение:
Смещение равно 2.
Таблица 1 - Исходные данные для расчетов
| № | Si | Si-l |
| 1 | 0,83 | |
| 2 | 0,98 | |
| 3 | 0,75 | 0,83 |
| 4 | 0,71 | 0,98 |
| 5 | 0,85 | 0,75 |
| 6 | 0,84 | 0,71 |
| 7 | 0,8 | 0,85 |
| 8 | 0,75 | 0,84 |
| 9 | 0,9 | 0,8 |
| 10 | 1 | 0,75 |
| 11 | 0,98 | 0,9 |
| 12 | 0,83 | 1 |
| 13 | 0,75 | 0,98 |
| 14 | 0,98 | 0,83 |
| 15 | 0,72 | 0,75 |
| 16 | 0,83 | 0,98 |
| 17 | 0,98 | 0,72 |
| 18 | 0,75 | 0,83 |
| 19 | 0,83 | 0,98 |
| 20 | 1 | 0,75 |
| 21 | 0,98 | 0,83 |
| 22 | 0,98 | 1 |
| 23 | 0,84 | 0,98 |
Получены следующие данные:
Количество значений - 23
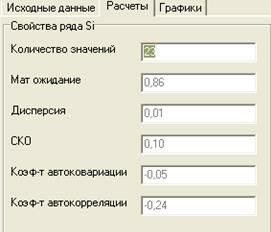
Вывод:
В ряде с 23 значениями отклонение от среднего составляет 0,1. Коэффициент автокорреляции -0,24, что свидетельствует об отсутствии зависимости между различными отсчетами содержания кремния в чугуне Si(i). Коэффициент автоковариации равен -0,05, что говорит об отсутствии линейной взаимосвязи между двумя отсчетами содержания кремния в чугуне Si(i). Дисперсия равная 0,01 характеризует низкую степень разброса значений содержания кремния в чугуне Si(i) относительно среднего значения. Математическое ожидание равное 0,86 означает, что среднее значение содержания кремния в чугуне Si(i) равно 0,86.
Полученные результаты нельзя считать объективно существующими на объекте поскольку данные для анализа были взяты случайным образом.
Провести сглаживание, фильтрацию и экстраполяцию стационарного случайного процесса
Дано:
1. Значения содержание кремния в чугуне Si(i).
2. Методика расчета фильтрации
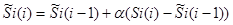
3. Методика расчета сглаживания
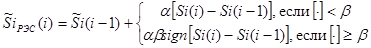
4. Методика расчета экстраполяции
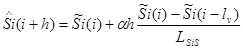
Требуется: провести сглаживание, фильтрацию и экстраполяцию случайного стационарного процесса при постоянной дисперсии при N=23
Решение:
1. Алгоритм проведения фильтрации:
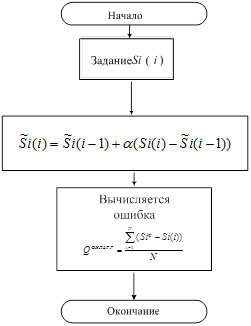
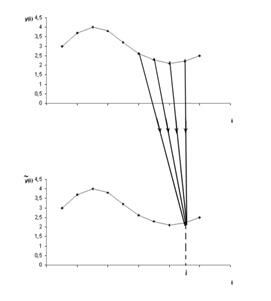
Рисунок 1 - Графическое отображение процедуры фильтрации
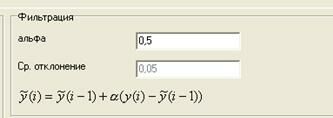
2. Алгоритм проведения сглаживания:
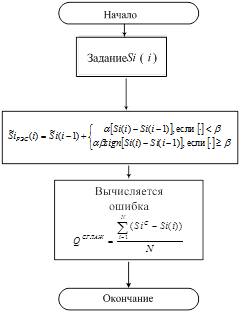
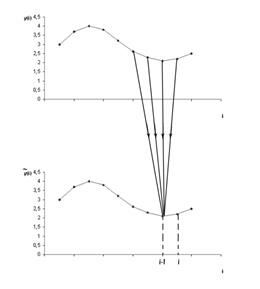
Рисунок 2 - Графическое отображение процедуры сглаживания
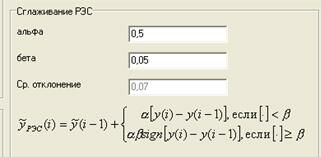
1. Алгоритм проведения экстраполяции:
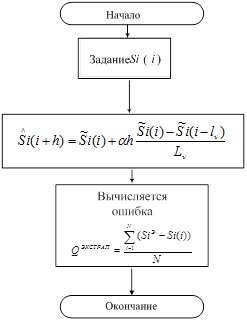
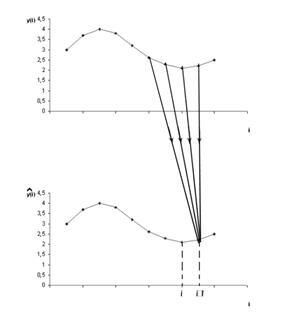
Рисунок 3 - Графическое отображение процедуры экстраполяции

Исходные данные и результаты расчетов представлены в таблице 2.
Таблица 2 – Исходные данные и результаты расчетов
| № | Si | Фильтрация | Сглаживание | Экстраполяция |
| 1 | 0,83 | 0,83 | 0,83 | 0,83 |
| 2 | 0,98 | 0,91 | 0,85 | 0,98 |
| 3 | 0,75 | 0,83 | 0,8 | 0,75 |
| 4 | 0,71 | 0,77 | 0,76 | 0,73 |
| 5 | 0,85 | 0,81 | 0,79 | 0,77 |
| 6 | 0,84 | 0,82 | 0,81 | 0,81 |
| 7 | 0,8 | 0,81 | 0,81 | 0,83 |
| 8 | 0,75 | 0,78 | 0,78 | 0,78 |
| 9 | 0,9 | 0,84 | 0,81 | 0,81 |
| 10 | 1 | 0,92 | 0,84 | 0,85 |
| 11 | 0,98 | 0,95 | 0,86 | 0,89 |
| 12 | 0,83 | 0,89 | 0,84 | 0,85 |
| 13 | 0,75 | 0,82 | 0,79 | 0,77 |
| 14 | 0,98 | 0,9 | 0,82 | 0,8 |
| 15 | 0,72 | 0,81 | 0,77 | 0,74 |
| 16 | 0,83 | 0,82 | 0,8 | 0,8 |
| 17 | 0,98 | 0,9 | 0,83 | 0,83 |
| 18 | 0,75 | 0,82 | 0,79 | 0,8 |
| 19 | 0,83 | 0,82 | 0,81 | 0,81 |
| 20 | 1 | 0,91 | 0,84 | 0,84 |
| 21 | 0,98 | 0,95 | 0,86 | 0,89 |
| 22 | 0,98 | 0,96 | 0,89 | 0,92 |
| 23 | 0,84 | 0,9 | 0,86 | 0,87 |
В графическом виде процедуры фильтрации, сглаживания и экстраполяции функции содержания кремния в чугуне представлены на рисунке 4.
Вместе с этой лекцией читают "8 Вывод на знаниях".
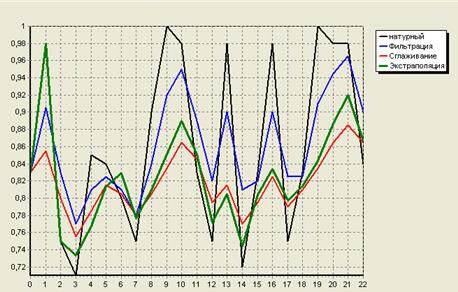
Рисунок 4 - Динамика формирования сглаженного, фильтрованного и экстраполированного выхода кремния в чугуне
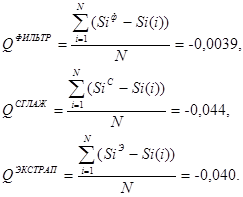
QФИЛЬТР – средняя ошибка фильтрации содержания кремния в чугуне;
QСГЛАЖ – средняя ошибка сглаживания содержания кремния в чугуне;
QЭКСТРАП – средняя ошибка экстраполяции содержания кремния в чугуне;






















