49221 (Теория игр), страница 3
Описание файла
Документ из архива "Теория игр", который расположен в категории "". Всё это находится в предмете "информатика" из 1 семестр, которые можно найти в файловом архиве . Не смотря на прямую связь этого архива с , его также можно найти и в других разделах. Архив можно найти в разделе "курсовые/домашние работы", в предмете "информатика, программирование" в общих файлах.
Онлайн просмотр документа "49221"
Текст 3 страницы из документа "49221"
Ожидаемый выигрыш 1 игрока если второй выбрал 2 стратегию:
А1 · 5 + (1 - p1) · 4 = А1 + 4;
6
5
4
2
0
1
- 4 А1 + 6 = А1 + 4
- 4 А1 + А1 = 4 – 6
- 5 А1 = - 2
А1 = 2/5 , А2 = 3/5.
Первому игроку для получения гарантированного выигрыша 4
,
(2/5+4) рекомендуется играть 1 стратегией.
Рассмотрим второго игрока.
Пусть В1 – вероятность выбора второй игрой 4 стратегией,
(В1 + В2 = 1, В2 = 1- В1)
Ожидаемый проигрыш второго игрока, если первый выберет 1 стратегию.
В1 · 2 + (1- В1) · 5 = - 3 В1 + 5
Ожидаемый проигрыш второго игрока, если первый выберет 2 стратегию.
В1 · 6 + (1- В1) · 4 = 2 В1 + 4
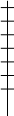
6
4
5
2
0
1
- 3 В1 + 5 = 2 В1 + 4
- 3 В1 – 2 В1 = 4 – 5
- 5 В1 = - 1
В1 = 1/5 , В2 = 4/5.
ν = 1/5 · 2 + 4 = 4
Ответ : Из 2 игр 2 надо сыграть 1 стратегией, 1 игру – 2 стратегией, и тогда проигрыш будет не больше 4 .
Пример 3: Решить игру, заданную матрицей
Проверим если ли седловая точка:
α = max (7,6) = 7
β = min (10,9,9) = 9 α ≠ β
седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков. Посмотрим, можно ли удалить не выгодную стратегию для игроков. Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.
| Невыгодная стратегия для второго игрока: | 3 |
p1
1 – p1
1 – p4
p4
Ожидаемый выигрыш 1 игрока, если второй выбрал 1 стратегию:
p1 · 7 + (1 - p1) · 10 = -3p1 + 10;
Ожидаемый выигрыш 1 игрока, если второй выбрал 2 стратегию:
p1 · 9 + (1 - p1) · 6 = 3 p1 + 6;
10
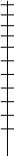
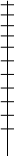
7
9
6
-3p1 + 10 = 3 p1 + 6
-3p1 - 3p1 = -10 + 6
-6p1 = -4
p1 = 2/3 , p2 =1/3 .
Первому игроку для получения гарантированного выигрыша 7
, (2/3+7) рекомендуется играть 1 стратегией.
Рассмотрим второго игрока.
Ожидаемые проигрыш второго игрока если первый выберет 1 стратегию.
p4 · 7 + (1- p4) · 9 = -2 p4 + 9
Ожидаемые проигрыш второго игрока если первый выберет 2 стратегию.
p4 · 10 + (1- p4) · 6 = 4 p4 + 6
9
10
6
7
0
1
-2p4 + 9 = 4 p4 + 6
-2p4 - 4p4 = 6 – 9
-6p4 = -3
р4 = 1/2 , p5 =1/2 .
Ответ : Из 2 игр (для первого) 2 надо сыграть 3 стратегией и 1 – 3 стратегией, (для второго) 1 надо сыграть 2 стратегией и 1 – 2 стратегией.
Пример 4: Решить игру, заданную матрицей
Проверим если ли седловая точка:
α = max (5,4,2,1) = 5
β = min (6,8) = 6 α ≠ β
седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков.
Посмотрим можно ли удалить не выгодную стратегию для игроков Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.
| Невыгодная стратегия для первого игрока: | 2,3 |
p1
1 - p1
1 – p4
р4
Ожидаемый выигрыш 1 игрока, если второй выбрал 1 стратегию:
p1 · 6 + (1 - p1) · 1 = 5 p1 + 1;
Ожидаемый выигрыш 1 игрока, если второй выбрал 2 стратегию:
p1 · 5 + (1 - p1) · 8 = -3 p1 + 8;
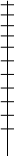
6
8
1
5
0
1
5 p1 + 1 = -3 p1 + 8
5 p1 + 3p1 = 8 – 1
8 p1 = 7
p1 = 7/8 , p2 =1/8 .
Рассмотрим второго игрока.
Ожидаемые проигрыш второго игрока, если первый выберет 1 стратегию.p4 · 6 + (1- p4) · 5 = p4 + 5
Ожидаемые проигрыш второго игрока, если первый выберет 2 стратегию.
p4 · 1 + (1- p4) · 8 = -7 p4 + 8
8
6
5
1
1
0
p4 + 5 = -7 p4 + 8
p4 + 7 p4 = 8 – 5
8 p4 = 3
р4 = 3/8 , p5 =5/8 .
= 
.
Ответ : Из 4 игр (для первого) 7 надо сыграть 8 стратегией и 1 – 8, (для второго) 3 надо сыграть 8 стратегией и 5 – 8.
4. Сведение задач теории игр к задачам линейного
программирования
Предположим, что цена игры положительна ( > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
Свойство 1. Тройка (хо, о, ) является решением игры = (Х,,А) тогда и только тогда, когда (хо, о, к +а) является решением игры (Х,,кА+а), где а любое вещественное число, к 0.
Свойство 2. Для того, чтобы хо = (
) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры , необходимо и достаточно выполнение следующих неравенств
(j = 
) 
Аналогично для игрока 2 : чтобы о = (
, ...,
, ...,
) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:
(i = 
) 
Из последнего свойства вытекает: чтобы установить, является ли предполагаемые (х, ) и решением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (*) и (**). С другой стороны, найдя неотрицательные решения неравенств (*) и (**) совместно со следующими уравнениями
, 
получим решение матричной игры.
Итак, пусть дана матричная игра с матрицей А порядка m х n. Согласно свойству 7 оптимальные смешанные стратегии х = (х1, ..., хm), y = (y1, ..., yn) соответственно игроков 1 и 2 и цена игры должны удовлетворять соотношениям.
Разделим все уравнения и неравенства в (4.4) и (4.5) на (это можно сделать, т.к. по предположению > 0) и введём обозначения:
, 
,
Тогда (1) и (2) перепишется в виде:
, 
, 
, ,
, 
, 
, .
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi , чтобы цена игры была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi , при которых
, . 
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, , при которых
, . 
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi , qj и .Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:
4.1 Решение задач
Пример 5: Найти решение игры, определяемой матрицей.
Решение.
Составим теперь пару взаимно-двойственных задач :
Решим вторую из них
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | Отношение | |
|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 3 | |
| | 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | — |
| q5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | — |
q4
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | Отношение | |
|
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | |
| | 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | — |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | Отношение | |
|
| | 0 | 0 | | 1 | 0 | | | |
| q2 | | 1 | 0 | | 0 | 0 | | | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | | 0 | 0 |
| 0 | 1 | | |
Из оптимальной симплекс-таблицы следует, что
(q1, q2, q3) = (0;
; 1),
а из соотношений двойственности следует, что
