183946 (743655)
Текст из файла
Размещено на http://www.allbest.ru/
Доверительный интервал.
Проверка статистических гипотез
1. Доверительный интервал
Точечные оценки являются приближенными, так как они указывают точку на числовой оси, в которой должно находиться значение неизвестного параметра. Однако оценка является приближенным значением параметра генеральной совокупности, которая при разных выборках одного и того же объема будет принимать разные значения, поэтому в ряде задач требуется найти не только подходящее значение параметра а, но и определить его точность и надежность.
Для этого в математической статистике используется два понятия – доверительный интервал и доверительная вероятность. Пусть для параметра а из опытных данных получена несмещенная оценка  Требуется определить возможную при этом величину ошибки и вероятность того, что оценка не выскочит за пределы этой ошибки (надежность).
Требуется определить возможную при этом величину ошибки и вероятность того, что оценка не выскочит за пределы этой ошибки (надежность).
Зададимся некоторой вероятностью (например, = 0,99) и найдем такое значение > 0, для которого

Представим это выражение в виде

Это значит, что с вероятностью точное значение параметра а находится в интервале l 
 l
l

Здесь параметр а – неслучайная величина, а интервал l является случайным, так как  - случайная величина. Поэтому вероятность лучше толковать, как вероятность того, что случайный интервал l накроет точку а. Интервал l называют доверительным интервалом, а вероятность - доверительной вероятностью (надежностью).
- случайная величина. Поэтому вероятность лучше толковать, как вероятность того, что случайный интервал l накроет точку а. Интервал l называют доверительным интервалом, а вероятность - доверительной вероятностью (надежностью).
Пример. Если при измерении какой-то величины Х указывается абсолютная погрешность х, то это, по существу, означает, что погрешность измерения, являясь случайной величиной, равномерно распределена в интервале (-х, х) и  где Х* - измеренная величина, а х – ее точное значение. Здесь = 1, = х и l = (x*- х, x* + х).
где Х* - измеренная величина, а х – ее точное значение. Здесь = 1, = х и l = (x*- х, x* + х).
-
Доверительный интервал для математического ожидания
В качестве еще одного примера рассмотрим задачу о доверительном интервале для математического ожидания. Пусть проведено n независимых опытов измерения случайной величины Х с неизвестным математическим ожиданием mx и дисперсией 2. На основании опытных данных Х1, Х2, ... , Хn построим выборочные оценки

Требуется построить (найти) доверительный интервал l, соответствующий доверительной вероятности , для среднего генерального mx.
Так как среднее выборочное  представляет сумму n независимых одинаково распределенных случайных величин
представляет сумму n независимых одинаково распределенных случайных величин  то при достаточно большом объеме выборки согласно центральной предельной теоремы ее закон близок к нормальному. Существует эмпирическое правило, по которому при объеме выборки n 30 выборочное распределение можем считать нормальным.
то при достаточно большом объеме выборки согласно центральной предельной теоремы ее закон близок к нормальному. Существует эмпирическое правило, по которому при объеме выборки n 30 выборочное распределение можем считать нормальным.
Ранее было показано, что  Найдем теперь такую величину () > 0, для которой выполняется равенство
Найдем теперь такую величину () > 0, для которой выполняется равенство

Считая случайную величину  нормально распределенной, имеем
нормально распределенной, имеем

После замены  имеем
имеем

По табличным значениям функции Лапласа Ф*(z) находим аргумент, при котором она равна . Если этот аргумент обозначить Z, то тогда

Среднее квадратичное значение  приближенно можно заменить
приближенно можно заменить

 где
где 
Таким образом, доверительный интервал для среднего генерального равен:
l = 
Если пользоваться табличными значениями интеграла вероятностей

то доверительный интервал принимает вид
l = 
-
Распределение Стьюдента
При малом объеме выборки (n < 30) полученный доверительный интервал для среднего генерального, использующий нормальное распределение случайной величины  , может быть очень грубым.
, может быть очень грубым.
Для более точного получения доверительного интервала необходимо знать закон распределения случайной величины  при малом объеме выборки. Для этого воспользуемся следующим результатом. Пусть Х1, Х2, ... , Хn – выборка нормально распределенной случайной величины Х, тогда, как доказано, случайная величина
при малом объеме выборки. Для этого воспользуемся следующим результатом. Пусть Х1, Х2, ... , Хn – выборка нормально распределенной случайной величины Х, тогда, как доказано, случайная величина

подчиняется распределению Стьюдента c n – 1 степенью свободы, плотность распределения которого имеет вид

где  - гамма функция. Эта плотность, как видно из формулы, зависит только от числа опытов n. Ниже представлены графики плотностей нормированной (mx = 0, = 1) нормально распределенной и с распределением Стьюдента (n = 4) случайных величин.
- гамма функция. Эта плотность, как видно из формулы, зависит только от числа опытов n. Ниже представлены графики плотностей нормированной (mx = 0, = 1) нормально распределенной и с распределением Стьюдента (n = 4) случайных величин.

нормальное распределение
f 
распределение Стьдента
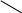 0,4
0,4 0,3
0,2
0,1
-4 -3 -2 -1 1 2 3 4 t
На основании найденных  можно, пользуясь распределением Стьюдента, найти доверительный интервал для mx , соответствующий доверительной вероятности . Действительно, так как
можно, пользуясь распределением Стьюдента, найти доверительный интервал для mx , соответствующий доверительной вероятности . Действительно, так как  то
то


Пользуясь таблицей значений интеграла

по значению найдем величину  а следовательно, и сам доверительный интервал l =
а следовательно, и сам доверительный интервал l = 
-
Проверка статистических гипотез
Принятие решения о параметрах генеральной совокупности играет исключительно важную роль на практике. Рассмотрим вопрос о принятии решения на примере. Пусть фирма, выпускающая конденсаторы, утверждает, что среднее пробивное напряжение конденсаторов равно или превышает 300 В. Испытав 100 конденсаторов, мы получили, что среднее выборочное пробивное напряжение равно 290 В, а несмещенное выборочное среднее квадратичное отклонение n = 40 В. Можно ли с доверительной вероятностью 0,99 утверждать, что среднее пробивное напряжение превышает 300 В.
Здесь нас интересует односторонняя оценка – среднее пробивное напряжение должно превышать 300 В.
Выскажем статистическую гипотезу – генеральное среднее mx = 300 В, а затем проверим, соответствует ли она результатам наблюдения. Поскольку объем выборки больше 30, то выборочное среднее можно считать гауссовской случайной величиной с генеральной дисперсией 2 n2. Введем центрированную и нормированную величину

Утверждение о том, что среднее выборочное напряжение  эквивалентно утверждению, что случайная величина
эквивалентно утверждению, что случайная величина

Найдем вероятность того, что гауссовская случайная величина Z с mz = 0 и z = 1 принимает значения больше zo:

Эта величина должна равняться доверительной вероятности 0,99. Тогда  и по таблицам значений функции
и по таблицам значений функции  находим аргумент zo = -2,33. Вычислим теперь наблюдаемое значение случайной величины Z:
находим аргумент zo = -2,33. Вычислим теперь наблюдаемое значение случайной величины Z:

Мы видим, что наблюдаемое значение z = - 2,5 нe принадлежит интервалу [-2,33;), поэтому гипотезу нужно отвергнуть.
Приведем пример гипотезы с двухсторонней оценкой. Пусть фирма, выпускающая стабилитроны определенного типа, утверждает, что номинальное напряжение стабилизации стабилитронов равно 10 В. Естественно, что отклонение напряжения стабилизации в меньшую или большую стороны одинаково нежелательно. Выдвинем гипотезу, что генеральное среднее напряжение стабилизации равно 10 В, а затем проверим эту статистическую гипотезу по результатам наблюдения.
Пусть при испытании 100 стабилитронов среднее выборочное равно 10,3 В, а несмещенное выборочное среднее квадратичное отклонение равно 1,2 В. Можно ли с доверительной вероятностью 0,95 считать выдвинутую гипотезу справедливой? Так как объем выборки больше 30, то можно, как и в предыдущем примере, ввести гауссовскую случайную величину Z. Найдем

и приравняем правую часть полученного соотношения 0,95. Тогда  и zo =1,96. Это значит, что наблюдаемое значение z должно принадлежать интервалу (-1,96; 1,96). Поскольку
и zo =1,96. Это значит, что наблюдаемое значение z должно принадлежать интервалу (-1,96; 1,96). Поскольку 
 не попадает в указанный интервал, то гипотеза отвергается.
не попадает в указанный интервал, то гипотеза отвергается.
Если объем выборки n < 30, то случайная величина  cчитается стьюденской случайной величиной T. Поэтому повторяя все указанные выше выкладки для проверки статистических гипотез, значения аргумента ищутся для распределения Стьюдента. При этом, так как "хвосты" стьюденского распределения по отношению к гауссовским удлиняются, доверительные интервалы расширяются, а возможности принятия гипотез улучшаются.
cчитается стьюденской случайной величиной T. Поэтому повторяя все указанные выше выкладки для проверки статистических гипотез, значения аргумента ищутся для распределения Стьюдента. При этом, так как "хвосты" стьюденского распределения по отношению к гауссовским удлиняются, доверительные интервалы расширяются, а возможности принятия гипотез улучшаются.
-
Функция риска
доверительный интервал вероятность статистическая гипотеза
Пусть имеются две противоположные гипотезы Но и Н1 и некоторая связанная с ними случайная величина Y. И пусть у - значение случайной величины Y, полученное в результате испытаний, которое принадлежит множеству - множество всех значений случайной величины Y. Требуется провести проверку гипотезы Но относительно конкурирующей гипотезы Н1 на основании результатов испытания.
Разобьем множество на две части - о и 1 с условием принятия гипотезы Но при попадании полученного значения у в о и гипотезы Н1 - при попадании у в 1. Выбор решающего правила, то есть разбиение множества на две части о и 1 в любой задаче проверки гипотез возможен больше, чем одним способом. Возникает вопрос, какое из этих разбиений в каждой конкретной задаче считать наилучшим? Чтобы решить поставленную задачу нужно обладать некоторой дополнительной информацией. Такая информация носит название априорной.
Будем считать известными два условных распределения вероятностей случайной величины Y:
 - плотность распределения случайной величині Y при условии, что верна гипотеза Но;
- плотность распределения случайной величині Y при условии, что верна гипотеза Но;
 - плотность распределения случайной величині Y при условии, что верна гипотеза Н1;
- плотность распределения случайной величині Y при условии, что верна гипотеза Н1;
Кроме того нам потребуется априорная вероятность р того, что гипотеза Но имеет место.
Введем в рассмотрение события:
А – верна гипотеза Но, тогда р = р(А);
 – верна конкурирующая гипотеза Н1, тогда р(
– верна конкурирующая гипотеза Н1, тогда р( ) = 1 - р;
) = 1 - р;
В – в результате эксперимента значение у попало в интервал о;
 – в результате эксперимента значение у попало в интервал 1.
– в результате эксперимента значение у попало в интервал 1.
Тогда по результатам эксперимента возможны только четыре события:
АВ – верна гипотеза Но и принято решение о ее истинности;
Характеристики
Тип файла документ
Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.
Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.
Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.















