Для студентов по предмету Математический анализТФКП и операционное исчисление (Чудесенко В.Ф.)ТФКП и операционное исчисление (Чудесенко В.Ф.)
4,9851353
2023-05-262023-05-26СтудИзба
ДЗ 1: ТФКП и операционное исчисление (Чудесенко В.Ф.) вариант 13
Описание
В этом варианте представлены следующие 26 задач:
задача №1, вариант 13
Найти все значения корня
![]()
задача №2, вариант 13
Представить в алгебраической форме
![]()
задача №3, вариант 13
Представить в алгебраической форме
![]()
задача №4, вариант 13
Вычертить область, заданную неравенствами
![]()
задача №5, вариант 13
Определить вид кривой
![]()
задача №6, вариант 13
Восстановить аналитическую в окрестности точки z0 функцию ƒ(z) по известной действительной части u(x, y) или мнимой υ(x, y) и значению ƒ(z0)
![]()
задача №7, вариант 13
Вычислить интеграл от функции комплексного переменного по данной кривой
![]()
задача №8, вариант 13
Найти все лорановские разложения данной функции по степеням Z
![]()
задача №9, вариант 13
Найти все Лорановские разложения данной функции по степеням z-z0
![]()
задача №10, вариант 13
Данную функцию разложить в ряд Лорана в окрестности точки z0
![]()
задача №11, вариант 13
Определить тип особой точки z=0 для данной функции
![]()
задача №12, вариант 13
Для данной функции найти изолированные точки и определить их тип
![]()
задача №13, вариант 13
Вычислить интеграл
![]()
задача №14, вариант 13
Вычислить интеграл
![]()
задача №15, вариант 13
Вычислить интеграл
![]()
задача №16, вариант 13
Вычислить интеграл
![]()
задача №17, вариант 13
Вычислить интеграл
![]()
задача №18, вариант 13
Вычислить интеграл
![]()
задача №19, вариант 13
Вычислить интеграл
![]()
задача №20, вариант 13
Вычислить интеграл
![]()
задача №21, вариант 13
По данному графику оригинала найти изображение
![]()
задача №22, вариант 13
Найти оригинал по заданному изображению
![]()
задача №23, вариант 13
Найти решение дифференциального уравнения, удовлетворяющего условиям y(0) = 0, y'(0) = 0
![]()
задача №24, вариант 13
Операционным методом решить задачу Коши
![]()
задача №25, вариант 13
Материальная точка массы m движется прямолинейно, отталкиваясь от начала координат с силой F = kx, пропорциональной расстоянию. На точку действует сила сопротивления среды R = rυ, пропорциональная скорости υ. При t = 0 расстояние точки от начала координат x0 а скорость υ0 Найти закон движения x = x(t) материальной точки.
![]()
задача №26, вариант 13
Решить систему дифференциальных уравнений
![]()
задача №1, вариант 13
Найти все значения корня
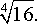
задача №2, вариант 13
Представить в алгебраической форме
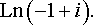
задача №3, вариант 13
Представить в алгебраической форме
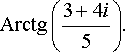
задача №4, вариант 13
Вычертить область, заданную неравенствами
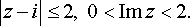
задача №5, вариант 13
Определить вид кривой

задача №6, вариант 13
Восстановить аналитическую в окрестности точки z0 функцию ƒ(z) по известной действительной части u(x, y) или мнимой υ(x, y) и значению ƒ(z0)

задача №7, вариант 13
Вычислить интеграл от функции комплексного переменного по данной кривой

задача №8, вариант 13
Найти все лорановские разложения данной функции по степеням Z
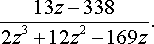
задача №9, вариант 13
Найти все Лорановские разложения данной функции по степеням z-z0
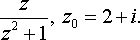
задача №10, вариант 13
Данную функцию разложить в ряд Лорана в окрестности точки z0
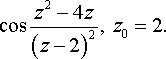
задача №11, вариант 13
Определить тип особой точки z=0 для данной функции
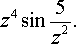
задача №12, вариант 13
Для данной функции найти изолированные точки и определить их тип

задача №13, вариант 13
Вычислить интеграл

задача №14, вариант 13
Вычислить интеграл

задача №15, вариант 13
Вычислить интеграл

задача №16, вариант 13
Вычислить интеграл

задача №17, вариант 13
Вычислить интеграл

задача №18, вариант 13
Вычислить интеграл

задача №19, вариант 13
Вычислить интеграл

задача №20, вариант 13
Вычислить интеграл

задача №21, вариант 13
По данному графику оригинала найти изображение

задача №22, вариант 13
Найти оригинал по заданному изображению

задача №23, вариант 13
Найти решение дифференциального уравнения, удовлетворяющего условиям y(0) = 0, y'(0) = 0
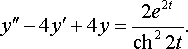
задача №24, вариант 13
Операционным методом решить задачу Коши

задача №25, вариант 13
Материальная точка массы m движется прямолинейно, отталкиваясь от начала координат с силой F = kx, пропорциональной расстоянию. На точку действует сила сопротивления среды R = rυ, пропорциональная скорости υ. При t = 0 расстояние точки от начала координат x0 а скорость υ0 Найти закон движения x = x(t) материальной точки.

задача №26, вариант 13
Решить систему дифференциальных уравнений
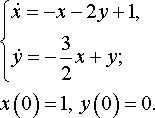
Характеристики домашнего задания
Предмет
Номер задания
Вариант
Теги
Просмотров
14
Качество
Скан рукописных листов
Размер
3,27 Mb
Список файлов
I-01-13.jpg
I-02-13.jpg
I-03-13.jpg
I-04-13.jpg
I-05-13.jpg
I-06-13.jpg
I-07-13.jpg
I-08-13.jpg
I-09-13.jpg
I-10-13.jpg
I-11-13.jpg
I-12-13.jpg
I-13-13.jpg
I-14-13.jpg
I-15-13.jpg
I-16-13.jpg
I-17-13.jpg
I-18-13.jpg
I-19-13.jpg
I-20-13.jpg
I-21-13.jpg
I-22-13.jpg
I-23-13.jpg
I-24-13.jpg
I-25-13.jpg
I-26-13.jpg
Комментарии
Нет комментариев
Стань первым, кто что-нибудь напишет!
 dmitry0376
dmitry0376






















