Для студентов МФПУ «Синергия» по предмету Математическая логика и теория алгоритмовМатематическая логика и теория алгоритмовМатематическая логика и теория алгоритмов
5,0053
2025-10-082025-10-08СтудИзба
Ответы к зачёту: Математическая логика и теория алгоритмов
Описание
Перед покупкой сверьте список вопросов и убедитесь, что вам нужны ответы именно на эти вопросы!
С вопросами и вы можете ознакомиться ДО покупки.
Для быстрого поиска вопроса используйте Ctrl+F.
С вопросами и вы можете ознакомиться ДО покупки.
Для быстрого поиска вопроса используйте Ctrl+F.
Список вопросов
Подмножество, составленное из элементов некоторого конечного множества, называют … данного множества.
Граф называется …, если для каждой вершины графа найдется маршрут начинающейся и заканчивающей в этой вершине и проходящий через все вершины только один раз (при этом могут участвовать не все ребра).
Всякое множество, элементам которого можно поставить во взаимно однозначное соответствие множество натуральных чисел, называется …
Какое из тождеств носит название «Закон де Моргана»?
Формулы, в которых очередной член последовательности выражается через один или несколько предыдущих членов, называются … соотношениями.
Пересечением числового отрезка [0, 4] с числовым отрезком [2, 5] является числовой отрезок
Установите последовательность операций в выражении по убыванию их приоритета: ![]()
![]()
![]()
![]()
![]()




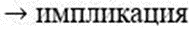
Произведение всех натуральных чисел от 1 до n называют … числа n.
Метод производящих функций был разработан
Элементарная конъюнкция называется …, если в неё каждая переменная входит не более одного раза, включая её вхождение и под знаком отрицания.
Для связного плоского графа, где V – количество вершин графа, E – количество ребер графа, F – количество граней графа, справедлива формула Эйлера:
Какое из предложений не является высказыванием?
Согласно теореме Кэли, число деревьев, которые можно построить на 4-х нумерованных вершинах будет равно:
Даны следующие производящие функции
![]()
![]()
![]()
![]()
![]()





Если полный граф имеет n вершин, то количество рёбер будет равно
Вставьте недостающие слова в определения в правильной последовательности. «Матрица … – это … матрица, в которой и число строк, и число столбцов равно n – числу … графа. Матрица … – это матрица размера n x m, где n – число вершин графа, m – число рёбер графа»
смежности
квадратная
вершин
инцидентности
смежности
квадратная
вершин
инцидентности
Даны два множества: А = {1, 2, 3}, B = {4, 5}. Укажите Декартово (прямое) произведение множеств А и В.
Множество формул алгебры логики называется …, если при всяком наборе значений переменных, входящих в эти формулы, по крайней мере одна из формул принимает значение 0.
Установите соответствие между графом, представленным на рисунке и матрицей смежности
A.![]()
B.![]()
C.![]()
D.![]()
E.![]()
F.![]()
G.![]()
H.![]()
A.

B.

C.

D.

E.

F.

G.

H.

Число ребер на дереве с 6-ю вершинами будет равно
Число различных булевых (логических) функций, зависящих от n переменных вычисляется по формуле: ![]()
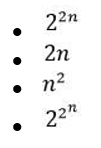
Укажите операцию, не относящуюся к основным алгебраическим операциям над множествами:
Расположите недостающие слова в формулировке теоремы Кантора-Бернштейна в правильном порядке
![]() инъективные
инъективные
отображения
биекция
равномощны
 инъективные
инъективные отображения
биекция
равномощны
Какое из рекуррентных соотношений указанных ниже является линейным?
Какая из указанных последовательностей, не является разбиением числа 5?
Элементарная дизъюнкция называется ____ относительно переменных x, y, z, ..., если в неё входит каждая из этих переменных не менее одного раза, включая и их вхождение под знаком отрицания.
Установите соответствие между формулой и названием закона алгебры множеств:
![]() A. 1
A. 1
B. 2
C. 3
D. 4
E. в
F. а
G. г
H. б
 A. 1
A. 1 B. 2
C. 3
D. 4
E. в
F. а
G. г
H. б
Установите соответствие между условием задачи и методом её решения:
A. На тарелке лежат 5 груш и 4 яблока. Сколькими способами можно выбрать один фрукт?
B. В канцелярском магазине продают 5 видов шариковых ручек и 4 вида тетрадей. Сколькими способами можно выбрать набор из ручки и тетради (т.е. одну ручку и одну тетрадь)?
C. Каждый ученик класса побывал в театре или в кино. В театр сходили 22 человека. В кино были 15 человек. И в театре, и в кино были 7 человек. Сколько учеников в классе?
D. Сколькими способами можно развесить 5 цветных шаров на гирлянде?
E. Правило суммы
F. Правило произведения
G. Формула включений и исключений для двух множеств
H. Формула перестановки
A. На тарелке лежат 5 груш и 4 яблока. Сколькими способами можно выбрать один фрукт?
B. В канцелярском магазине продают 5 видов шариковых ручек и 4 вида тетрадей. Сколькими способами можно выбрать набор из ручки и тетради (т.е. одну ручку и одну тетрадь)?
C. Каждый ученик класса побывал в театре или в кино. В театр сходили 22 человека. В кино были 15 человек. И в театре, и в кино были 7 человек. Сколько учеников в классе?
D. Сколькими способами можно развесить 5 цветных шаров на гирлянде?
E. Правило суммы
F. Правило произведения
G. Формула включений и исключений для двух множеств
H. Формула перестановки
Установите соответствие между определением понятия и его характеристикой
A. Формула алгебры логики называется …, если она принимает значение 1 при всех значениях входящих в неё элементарных переменных высказываний.
B. Формула алгебры логики называется …, если она принимает значение 0 при любых значениях входящих в неё элементарных переменных высказываний.
C. Формула алгебры логики называется …, если она принимает одно значение 1 хотя бы на одном наборе значений входящих в неё элементарных переменных высказываний.
D. Формула алгебры логики называется …, если она принимает одно значение 0 хотя бы на одном наборе значений входящих в неё элементарных переменных высказываний.
E. тавтологией
F. противоречием
G. выполнимой
H. опровержимой
A. Формула алгебры логики называется …, если она принимает значение 1 при всех значениях входящих в неё элементарных переменных высказываний.
B. Формула алгебры логики называется …, если она принимает значение 0 при любых значениях входящих в неё элементарных переменных высказываний.
C. Формула алгебры логики называется …, если она принимает одно значение 1 хотя бы на одном наборе значений входящих в неё элементарных переменных высказываний.
D. Формула алгебры логики называется …, если она принимает одно значение 0 хотя бы на одном наборе значений входящих в неё элементарных переменных высказываний.
E. тавтологией
F. противоречием
G. выполнимой
H. опровержимой
Установите соответствие между операцией над высказываниями и её определением:
A. Конъюнкция
B. Эквиваленция
C. Импликация
D. Дизъюнкция
E. Логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания
F. Логическая операция, образующая сложное высказывание, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность.
G. Логическая операция, которая двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда из истины следует ложь.
H. Логическая операция, образующая сложное высказывание, истинное в том случае, когда хотя бы одно из высказываний истинно
A. Конъюнкция
B. Эквиваленция
C. Импликация
D. Дизъюнкция
E. Логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания
F. Логическая операция, образующая сложное высказывание, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность.
G. Логическая операция, которая двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда из истины следует ложь.
H. Логическая операция, образующая сложное высказывание, истинное в том случае, когда хотя бы одно из высказываний истинно
Установите соответствие между названием специального числа и его характеристикой.
A. Числа Стирлинга второго рода
B. Числа Люкаса
C. Числа Белла
D. Числа Фибоначчи
E. представляют собой число разбиений k-элементного множества на n частей.
F.![]() G. представляют собой количество разбиений множества из n элементов на произвольное количество непустых подмножеств, которые не пересекаются.
G. представляют собой количество разбиений множества из n элементов на произвольное количество непустых подмножеств, которые не пересекаются.
H.![]()
A. Числа Стирлинга второго рода
B. Числа Люкаса
C. Числа Белла
D. Числа Фибоначчи
E. представляют собой число разбиений k-элементного множества на n частей.
F.
 G. представляют собой количество разбиений множества из n элементов на произвольное количество непустых подмножеств, которые не пересекаются.
G. представляют собой количество разбиений множества из n элементов на произвольное количество непустых подмножеств, которые не пересекаются. H.

Установите соответствие между действием, выполняемым над множеством и обозначением этого действия с помощью диаграммы Эйлера-Венна
A.![]()
B.![]()
C.![]() D.
D. ![]()
E.![]() F.
F. ![]() G.
G. ![]() H.
H. ![]()
A.

B.

C.
 D.
D. 
E.
 F.
F.  G.
G.  H.
H. 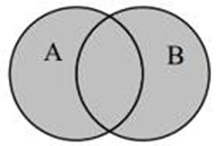
Установите соответствие между видом графа и его определением.
A. Полный граф
B. Нулевой граф
C. Регулярный граф
D. Связный граф
E. граф, в котором проведены все возможные ребра.
F. граф, состоящий только из изолированных вершин, т.е. граф, не содержащий ни одного ребра.
G. связный граф, все вершины которого имеют одинаковую степень.
H. граф, между любыми вершинами которого существует путь.
A. Полный граф
B. Нулевой граф
C. Регулярный граф
D. Связный граф
E. граф, в котором проведены все возможные ребра.
F. граф, состоящий только из изолированных вершин, т.е. граф, не содержащий ни одного ребра.
G. связный граф, все вершины которого имеют одинаковую степень.
H. граф, между любыми вершинами которого существует путь.
Расположите указанные логические следствия схемы доказательств в следующем порядке: доказательство разбором случаев, доказательство построением цепочки импликаций, доказательство от противного или метод косвенного доказательства, доказательство теорем типа «если х, то у»
![]()
![]()
![]()
![]()



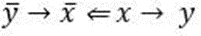
Расположите недостающие слова в определении в правильном порядке: ![]() рефлексивным
рефлексивным
симметричным
антисимметричным
транзитивным
 рефлексивным
рефлексивным симметричным
антисимметричным
транзитивным
Расположите его вершины в порядке увеличения их степени, т. е. от меньшей степени к большей.
![]()
D
C
B
A

D
C
B
A
Операции, при выполнении которых появляются новые элементы, называют … операциями.
Множество 2A называется … множества A.
Даны четыре линейных рекуррентных соотношения.
![]() Запишите их по следующему правилу: от рекуррентного соотношения меньшего порядка до рекуррентного соотношения большего порядка.
Запишите их по следующему правилу: от рекуррентного соотношения меньшего порядка до рекуррентного соотношения большего порядка.
an + 2 = 4an+1 – 3
an + 2 = 3an+1 + 2an
an + 2 = 2an+1 – 3an + 2an-1
an + 2 = 4an+1 – 2an + 3an-1 - an-2
 Запишите их по следующему правилу: от рекуррентного соотношения меньшего порядка до рекуррентного соотношения большего порядка.
Запишите их по следующему правилу: от рекуррентного соотношения меньшего порядка до рекуррентного соотношения большего порядка. an + 2 = 4an+1 – 3
an + 2 = 3an+1 + 2an
an + 2 = 2an+1 – 3an + 2an-1
an + 2 = 4an+1 – 2an + 3an-1 - an-2
Граф является … тогда и только тогда, когда степени всех его вершин четные.
Характеристики ответов (шпаргалок) к зачёту

❓ Как копировать вопросы во время теста в Синергии?
Комментарии
Нет комментариев
Стань первым, кто что-нибудь напишет!
 МФПУ «Синергия»
МФПУ «Синергия»  shalenysh
shalenysh


















