Для студентов МГТУ им. Н.Э.Баумана по предмету Математическая логика и теория алгоритмовМЛиТА решенные билеты к сессииМЛиТА решенные билеты к сессии
5,00595
2024-09-042025-04-03СтудИзба
Ответы к экзамену: МЛиТА решенные билеты к сессии
Описание
1)
![]()
![]()
![]()
![]()
- Понятие «задача». Форма задачи. Индивидуальная и массовая задача. Примеры.
- Построить сведение задачи «Гамильтонов цикл» к задаче «Коммивояжер».
- Приближенные алгоритмы с оценкой точности. Теорема об ԑ-приближенном алгоритме для задачи коммивояжера.
- Определение Машины Тьюринга (МТ). Различие детерминированной и недетерминированной МТ. Определение понятия «сложность» (трудоемкость) вычисления для обоих случаев. Привести примеры вычисления для обоих случаев.
- Построить сведение задачи «КНФ-выполнимость» к задаче «Клика».
- Дать определение СФЭ в общем случае. Привести пример.
- Определение Оракульной Машины Тьюринга (ОМТ). Различие оракульной и недетерминированной МТ.
- Доказать нижнюю оценку функции Шеннона для СФЭ в базисе «¬, ˄, ˅».
- Построить сведение задачи «КНФ-выполнимость» к задаче «Клика».
- Определение Недерминированной Машины Тьюринга (НМТ). Различие оракульной и недетерминированной МТ.
- Доказать оценку функции Шеннона для СФЭ, реализующей все конъюнкции от n переменных.
- Построить сведение задачи «Гамильтонов цикл» к задаче «Коммивояжер».
- Задание «входа» для индивидуальной задачи. Примеры кодировок графов. Понятие полиномиальной эквивалентности для различных кодировок объекта.
- Построить алгорифм Маркова сложения двух чисел в алфавите «*,1».
- Дать определение классов EXPTIME и PSPACE. Доказать утверждение о соотношении между ними.
- Классы PSPASE, NPSPASE. Соотношение между ними.
- Построить СФЭ минимальной сложности для функции (00110101) в базисе «¬, ˄, ˅».
- Теорема о PSPACE-полной задаче.
- Классы PSPASE, NPSPASE. Соотношение между ними.
- Построить СФЭ минимальной сложности для функции (00110101) в базисе «¬, ˄, ˅».
- Теорема о PSPACE-полной задаче.
- Классы PSPASE, EXPTIME. Соотношение между ними.
- Построить минимальную СФЭ для функции (01110100).
- Доказать оценку функции Шеннона для СФЭ, реализующей все конъюнкции от n переменных.
- Определение СФЭ в базисе «¬, ˄, ˅». Привести пример СФЭ.
- Построить МТ для обращения слов в заданном алфавите.
- Теорема Кука. Идея и схема доказательства.
- Классы P/Poly и P. Теорема о соотношении между ними.
- Построить НАМ для обращения слов в заданном алфавите.
- Доказать оценку сверху для функции Шеннона L(n)≤(n +1) 2n.
- Класс PSPASE и игра двух лиц. Теорема о соотношении между ними.
- По заданной формуле в исчислении предикатов построить формулу в приведенной нормальной форме. Сформулировать теорему о длине формулы в исчислении предикатов.
- Понятие РАМ (Равнодоступная Адресная Машина). Привести пример.
- Двуместные отношения и сводимость по Тьюрингу. NP-трудные задачи. Привести пример.
- Привести примеры полиномиально разрешимых частных случаев NP –полных задач.
- Доказать оценку сверху для функции Шеннона L(n) <12•2n / n.
- Дать определения и привести примеры следующих понятий в исчислении предикатов: Предикат. Формула в исчислении предикатов. Выполнимые и общезначимые формулы. Приведенная нормальная форма.
- Определить классы сложности для задач «К-е по порядку множество», «Задача о камнях».
- Доказать оценку L(n)> 2n / n.
- Теорема Кука. Идея и схема доказательства.
- Построить СФЭ для функции (11100101).
- Понятие «коммуникационная сложность». Коммуникационная сложность задачи о равенстве числа единиц в двух булевских векторах.
- Понятие алгоритма. Понятие эквивалентность алгоритмов. Тезис Черча.
- Алгоритм нахождения кратчайшего пути между вершинами графа.
- Доказать оценку сверху для функции Шеннона L(n) <12•2n / n.
- Примеры подходов к решению NP-полных задач: полиномиально разрешимые частные случаи, псевдополиномиальные алгоритиы, алгоритмы с оценкой точности.
- Определение полиномиальной сводимости и сводимости по Тьюрингу. Привести пример полиномиальной сводимости и сводимости по Тьюрингу.
- Построить МТ для вычисления x-y.
- Теорема о PSPACE-полной задаче.
- Построить минимальную СФЭ для функции (11100101). (Базис задает преподаватель.)
- Построить НАМ для вычисления x-y.
- Классы NP и co-NP. Соотношение между ними. Теорема об NP–полной задаче и классе Co-NP.
- Построить МТ для сложения чисел.
- Доказать оценку L(n)> 2n / n.
- Приближенные алгоритмы с оценкой точности. Теорема о существовании такого алгоритма для «Задачи коммивояжера».
- Игра двух лиц. Определение. Игра двух лиц и классы NP и co-NP.
- Определить классы сложности для задач «К-е по порядку множество», «Задача о камнях».
- Коммуникационная сложность. Коммуникационная сложность задачи о равенстве числа единиц в двух булевских векторах.
- По заданной формуле в исчислении предикатов построить формулу в приведенной нормальной форме.
- Теорема Кука. Идея и схема доказательства.



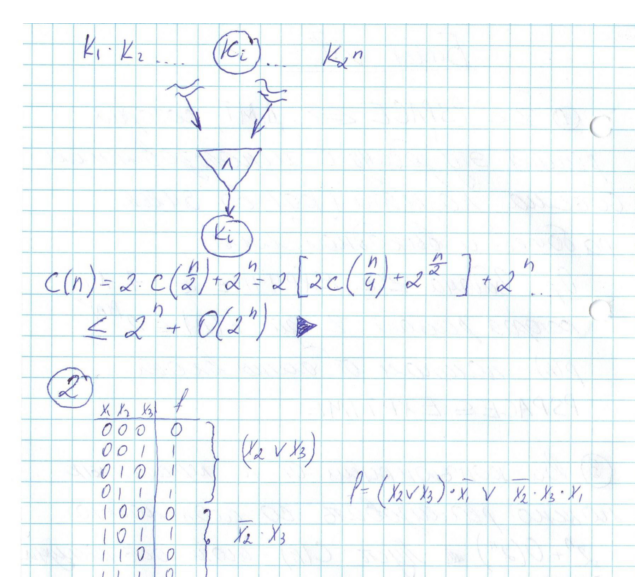
Характеристики ответов (шпаргалок) к экзамену
Учебное заведение
Семестр
Просмотров
13
Размер
68,27 Mb
Список файлов
Нечетные.docx
Ответы четные-нечетные.pdf
Четные.docx
Комментарии
Нет комментариев
Стань первым, кто что-нибудь напишет!
 МГТУ им. Н.Э.Баумана
МГТУ им. Н.Э.Баумана AlexInfinity
AlexInfinity

















