практикум_механика (1) (1106030), страница 9
Текст из файла (страница 9)
Эксперимент 1. Проверка линейного характера зависимости времени равномерного прямолинейного движения от пройденного телом пути
В первых двух экспериментах проверяется правомерность применения общего уравнения (7) кинематики для описания реального движения груза. Рассматриваются два частных случая. В первом эксперименте – случай равномерного движения  , когда ускорение
, когда ускорение  , а
, а  . Во втором – случай равноускоренного движения
. Во втором – случай равноускоренного движения  , когда
, когда  , а начальная скорость
, а начальная скорость  .
.
Практически в первом эксперименте удобнее проверять зависимость

где  – отрезок времени движения груза
– отрезок времени движения груза  на пути
на пути  со скоростью, которую он приобрел, пройдя ускоренно путь
со скоростью, которую он приобрел, пройдя ускоренно путь  .
.
Допустим, что зависимость (14) неизвестна, и предположим, что она имеет вид степенной функции

где  и
и  – константы.
– константы.
Цель эксперимента заключается в определении констант  и
и  . Прологарифмировав (15), получим зависимость
. Прологарифмировав (15), получим зависимость

график которой является прямой линией (рис.3).

Проведя серию измерений и построив график по рис.3, найдем искомые величины  и
и  . Величина
. Величина  определяется ординатой точки пересечения графика с вертикальной осью. Логарифмируя (14) и сравнивая его с (15), получим
определяется ординатой точки пересечения графика с вертикальной осью. Логарифмируя (14) и сравнивая его с (15), получим  , что позволяет найти скорость
, что позволяет найти скорость 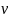 движения груза на участке
движения груза на участке  . Величина
. Величина  находится из соотношения
находится из соотношения

Если полученное значение  окажется близким к единице, это будет означать, что реальный характер движения груза на участке
окажется близким к единице, это будет означать, что реальный характер движения груза на участке  действительно описывается уравнением (14) равномерного прямолинейного движения тела.
действительно описывается уравнением (14) равномерного прямолинейного движения тела.
Экспериментально проводятся измерения времени  движения груза
движения груза  с надетым перегрузком типа
с надетым перегрузком типа 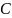 для серии значений пути
для серии значений пути  . При этом
. При этом  выбирается постоянным, чтобы величина скорости, приобретенной на этом участке, оставалась неизменной. Изменение величины
выбирается постоянным, чтобы величина скорости, приобретенной на этом участке, оставалась неизменной. Изменение величины  производится перемещением платформы 8. Для каждого значения
производится перемещением платформы 8. Для каждого значения  измерение времени движения производится не менее
измерение времени движения производится не менее  раз. Измерения повторяются для случая двух различных по массе перегрузков типа
раз. Измерения повторяются для случая двух различных по массе перегрузков типа 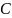 . Результаты измерений заносятся в таблицу 1. Производится статистическая обработка полученных результатов и строятся графики (рис.3) с указанием на нем доверительных интервалов. В зависимости от массы
. Результаты измерений заносятся в таблицу 1. Производится статистическая обработка полученных результатов и строятся графики (рис.3) с указанием на нем доверительных интервалов. В зависимости от массы  выбранного перегрузка типа
выбранного перегрузка типа 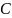 графики могут пересекать ось ординат выше оси абсцисс (прямая 1) или ниже ее (прямая 2). По графикам определяются величины
графики могут пересекать ось ординат выше оси абсцисс (прямая 1) или ниже ее (прямая 2). По графикам определяются величины  и
и  . Затем вычисляется соответствующее значение скорости и проводится анализ полученных результатов.
. Затем вычисляется соответствующее значение скорости и проводится анализ полученных результатов.
Таблица 1
|
[см] |
| |||||
| № |
|
|
|
| ||
|
| 1 2 3 4 5 | |||||
|
| ||||||
| ……. | …. | ………………. | …….. | ……….. | …….. | |
|
| ||||||
|
|
| |||||
|
| ||||||
|
| ||||||
|
| ||||||
|
|
|
| ||||
Эксперимент 2. Проверка квадратичного характера зависимости времени равноускоренного прямолинейного движения от пройденного телом пути
Поскольку экспериментальная установка не позволяет нам измерять время  движения груза на отрезке пути
движения груза на отрезке пути  , то мы не можем проверять непосредственно соотношение
, то мы не можем проверять непосредственно соотношение

Однако, воспользовавшись уравнением (6), представленным в виде  (при условии, что
(при условии, что  ), получим из (7) выражение
), получим из (7) выражение

где  – скорость, которую приобретает груз за время
– скорость, которую приобретает груз за время  прохождения пути
прохождения пути  , а эту скорость мы научились измерять в первом эксперименте. Заменив
, а эту скорость мы научились измерять в первом эксперименте. Заменив  на
на  (см (10)), получим зависимость времени
(см (10)), получим зависимость времени  , за которое груз проходит путь
, за которое груз проходит путь  равномерно, от величины пути
равномерно, от величины пути  его равноускоренного движения
его равноускоренного движения

Будем считать эту зависимость неизвестной и предположим, что она имеет степенной вид

где  и
и  – константы.
– константы.

Цель эксперимента – проверить является ли  константой и показать, что
константой и показать, что  . Прологарифмируем выражение (17) и получим соотношение
. Прологарифмируем выражение (17) и получим соотношение

График этой функции, представленный на рис.4, имеет вид прямой линии. Точка его пересечения с осью ординат определяет значение величины  , а тангенс угла наклона позволяет найти константу
, а тангенс угла наклона позволяет найти константу

Сняв экспериментальную зависимость  и построив соответствующий график в координатах
и построив соответствующий график в координатах  , необходимо с помощью линейки проверить, является ли график прямой линией, а затем по данным графика определить величину
, необходимо с помощью линейки проверить, является ли график прямой линией, а затем по данным графика определить величину  , а по формуле (18) значение коэффициента
, а по формуле (18) значение коэффициента  . Если график окажется прямой линией, а коэффициент
. Если график окажется прямой линией, а коэффициент  , это будет означать, что реальное движение груза было равноускоренным и может описываться уравнением (7).
, это будет означать, что реальное движение груза было равноускоренным и может описываться уравнением (7).
Экспериментально измеряется время  движения груза
движения груза  с надетым перегрузком типа
с надетым перегрузком типа 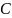 для серии значений пути
для серии значений пути  равноускоренного движения при
равноускоренного движения при  .
.
Таблица 2
|
[см] |
| |||||
| № |
|
|
|
| ||
|
| 1 2 3 4 5 | |||||
|
| ||||||
| ……. | …. | ………………. | …….. | ……….. | …….. | |
|
| ||||||
|
|
| |||||
|
| ||||||
|
| ||||||
|
| ||||||
|
|
| |||||
Изменение величины  производится перемещением платформы 6. Для каждого значения
производится перемещением платформы 6. Для каждого значения  время
время  измеряется не менее
измеряется не менее  раз. Измерения повторяются для двух различных по массе перегрузков типа
раз. Измерения повторяются для двух различных по массе перегрузков типа 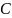 . Результаты измерений записываются в таблицу 2. Производится статистическая обработка полученных результатов и строятся графики (рис.4) с указанием доверительных интервалов. В зависимости от массы
. Результаты измерений записываются в таблицу 2. Производится статистическая обработка полученных результатов и строятся графики (рис.4) с указанием доверительных интервалов. В зависимости от массы  выбранного перегрузка типа
выбранного перегрузка типа 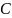 графики могут пересекать ось ординат выше оси абсцисс (прямая 1) или ниже (прямая 2). По графикам определяются величины
графики могут пересекать ось ординат выше оси абсцисс (прямая 1) или ниже (прямая 2). По графикам определяются величины  и
и  .
.
Эксперимент 3. Проверка второго закона динамики Ньютона
Машина Атвуда позволяет произвести изучение основного закона динамики Ньютона для поступательного прямолинейного движения системы грузов. На груз  поместим добавочный перегрузок типа
поместим добавочный перегрузок типа 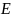 массы
массы  , компенсирующий трение. Положим на грузы
, компенсирующий трение. Положим на грузы  и
и  одинаковой массы
одинаковой массы  по одному перегрузку типа
по одному перегрузку типа  одинаковой массы
одинаковой массы  (вес каждого перегрузка
(вес каждого перегрузка  ) и, кроме того, на груз
) и, кроме того, на груз  положим перегрузок типа
положим перегрузок типа 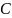 массы
массы  (его вес
(его вес  ). В этом случае вся система грузов на нити, перекинутой через блок, будет иметь массу
). В этом случае вся система грузов на нити, перекинутой через блок, будет иметь массу

Равнодействующая всех сил, приложенных к системе тел, равна  . Она сообщает всей системе ускорение
. Она сообщает всей системе ускорение  . Уравнение Ньютона, применительно к ускоренному движению рассматриваемой системы, запишется так
. Уравнение Ньютона, применительно к ускоренному движению рассматриваемой системы, запишется так

Если перегрузок типа  переложить с груза
переложить с груза  на груз
на груз  , то общая масса системы останется неизменной. Величина же равнодействующей силы увеличится и будет равна
, то общая масса системы останется неизменной. Величина же равнодействующей силы увеличится и будет равна  . В этом случае система получит другое, большее ускорение
. В этом случае система получит другое, большее ускорение  . Второй закон Ньютона для нее запишется следующим образом
. Второй закон Ньютона для нее запишется следующим образом

Деля (19) на (20), имеем

Соотношение (21) представляет собой следствие второго закона Ньютона применительно к системе грузов, движущихся равноускорено под действием силы тяжести. Ускорения  и
и  можно найти из выражения (16), использованного нами во втором эксперименте
можно найти из выражения (16), использованного нами во втором эксперименте

Ускорения  и
и  , с которыми система движется под действием сил
, с которыми система движется под действием сил  и
и  запишутся в виде
запишутся в виде

С учетом (22) отношение ускорений можно записать следующим образом

В пределах погрешности измерений отношение ускорений (23) должно равняться отношению сил, вызывавших эти ускорения (21). Это утверждение и подлежит экспериментальной проверке.
Эксперимент проводят в следующей последовательности. Расстояния  и
и  выбирают произвольно, но не меняют их в течение всего эксперимента. Компенсируют трение, подобрав величину массы
выбирают произвольно, но не меняют их в течение всего эксперимента. Компенсируют трение, подобрав величину массы  перегрузка типа
перегрузка типа 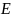 , надетого на груз
, надетого на груз  , по описанной выше методике. Для обеспечения ускорения
, по описанной выше методике. Для обеспечения ускорения  системы, на груз
системы, на груз  кладут один перегрузок типа
кладут один перегрузок типа  , а на груз
, а на груз  кладут сначала перегрузок типа
кладут сначала перегрузок типа  аналогичной массы, а сверху перегрузок типа
аналогичной массы, а сверху перегрузок типа 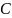 . Не менее
. Не менее  раз измеряют время
раз измеряют время  прохождения грузом
прохождения грузом  пути
пути  и результаты заносят в таблицу 3. Для получения ускорения
и результаты заносят в таблицу 3. Для получения ускорения  снимают с груза
снимают с груза  перегрузок типа
перегрузок типа  и перекладывают его на груз
и перекладывают его на груз  . Определяют новое время
. Определяют новое время  прохождения грузом
прохождения грузом  пути
пути  , а результаты заносят в таблицу 3. Проводят статистическую обработку полученных результатов, рассчитывают по формуле (23) отношение ускорений
, а результаты заносят в таблицу 3. Проводят статистическую обработку полученных результатов, рассчитывают по формуле (23) отношение ускорений  и его погрешность
и его погрешность  . Сравнивают отношение ускорений
. Сравнивают отношение ускорений  с отношением соответствующих сил (21). Результаты эксперимента считаются удовлетворительными, если выполняется соотношение
с отношением соответствующих сил (21). Результаты эксперимента считаются удовлетворительными, если выполняется соотношение

Таблица 3
|
[ |
| ||||||
| № |
|
|
|
| |||
|
| 1 2 3 4 5 | ||||||
|
| 1 2 3 4 5 | ||||||
|
|
|
| |||||
|
|
|
| |||||
|
| |||||||
|
| |||||||
ЛАБОРАТОРНАЯ РАБОТА 4
 [см],
[см],  [г]
[г] [c]
[c] [c]
[c] [c]
[c]








 [см],
[см], 






 ]
] [см];
[см];  [г]
[г]
















