Глава_3 (1085731), страница 3

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 3)

Максимальное количество открытых файлов также ограниченно размером таб­лицы i-узлов, следовательно, когда таблица заполняется целиком, возникает та же самая проблема. Пространство для подкачки файлов на диск является еще одним ограниченным ресурсом. Фактически почти каждая таблица в операционной сис­теме представляет собой ресурс, имеющий пределы. Должны ли мы упразднить их все из-за того, что может произойти ситуация, когда в группе из п процессов каждый может потребовать 1/п от целого, а затем попытаться получить еще часть?

Большая часть операционных систем, включая UNIX и Windows, игнорируют эту проблему. Они исходят из предположения, что большинство пользователей скорее предпочтут иметь дело со случающимися время от времени взаимоблоки­ровками, чем с правилом, по которому всем пользователям разрешается только один процесс, один открытый файл и т. д. Если бы можно было легко устранить взаимоблокировки, не возникло бы столько разговоров на эту тему. Сложность заключается в том, что цена достаточно высока, и в основном она, как мы вскоре увидим, исчисляется в наложении неудобных ограничений на процессы. Таким образом, мы столкнулись с неприятным выбором между удобством и корректнос­тью и множеством дискуссий о том, что более важно и для кого. При всех этих условиях трудно найти верное решение.

Обнаружение и устранение взаимоблокировок

Вторая техника представляет собой обнаружение и восстановление. При исполь­зовании этого метода система не пытается предотвратить попадание в тупиковые ситуации. Вместо этого она позволяет взаимоблокировке произойти, старается определить, когда это случилось, и затем совершает некие действия к возврату си­стемы к состоянию, имевшему место до того, как система попала в тупик. В этом разделе мы рассмотрим некоторые из способов обнаружения тупиковых ситуаций и выхода из них.

Обнаружение взаимоблокировки при наличии одного ресурса каждого типа

Начнем с самого простого варианта: в системе существует только один ресурс каж­дого типа. Подобная система могла бы иметь один сканер, одно устройство для за­писи компакт-дисков, один плоттер и один накопитель на магнитной ленте, то есть не более чем по одному представителю каждого класса. Другими словами, мы ис­ключаем из рассмотрения системы с двумя одновременно подключенными прин­терами. Мы обратимся к ним позже и будем использовать другой метод.

Для такой системы можно сконструировать граф ресурсов вида, продемонст­рированного на рис. 3.3. Если этот граф содержит один или больше циклов, зна­чит, произошла взаимоблокировка и блокирован любой процесс, являющийся частью цикла. Если в графе нет циклов, система не попала в тупик.

В качестве примера более сложной системы, чем те, которые мы рассматрива­ли до сих пор, обсудим систему с семью процессами, обозначенными буквами от Л до G, и шестью ресурсами, обозначенными буквами от R до W. Состояние систе­мы, то есть то, какой процесс владеет каким ресурсом и какой ресурс запрашива­ется процессом в данный момент, соответствует следующему списку:

1. Процесс А занимает ресурс R и хочет получить ресурс S.

2. Процесс В ничего не использует, но хочет получить ресурс Т.

3. Процесс С ничего не использует, но хочет получить ресурс S.

4. Процесс D занимает ресурс U и хочет получить ресурсы S и Т.

5. Процесс Е занимает ресурс Т и хочет получить ресурс V.

6. Процесс F занимает ресурс W и хочет получить ресурс S.

7. Процесс G занимает ресурс V u хочет получить ресурс U.

Вопрос: «Заблокирована ли эта система и если да, то какие процессы в этом участвуют?»

Чтобы ответить на этот вопрос, мы можем составить граф ресурсов (рис. 3.3, а). Этот граф содержит один цикл, который виден при визуальном обследовании. Цикл показан на рис. 3.3, б. Изучая его, можно заметить, что процессы D,E u G за­блокированы. Процессы Л, С и F нe попали в тупик, потому что любому из них можно предоставить ресурс S, после чего процесс, получивший ресурс, закончит свою работу и вернет ресурс. Затем два других процесса по очереди могут полу­чить ресурс и также успешно выполнить свою работу.

R

A

B

R

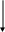
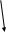
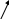
S

C

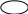
D

T

E

D

E

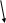
F

U

U

V

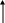
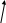
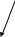
W

G

G

V

а б

Рис. 3.3. Граф ресурсов (а); цикл, извлеченный из а (б)

Несмотря на то что в простом графе относительно легко зрительно различить взаимоблокировку процессов, для использования такой схемы в настоящей систе­ме нам необходим формальный алгоритм, выявляющий тупики. Известно множе-

ство алгоритмов, обнаруживающих циклы в направленных графах. Ниже мы рас­смотрим простой алгоритм, который изучает граф и завершается или когда нахо­дит цикл, или когда показывает, что циклов в этом графе не существует. Он ис­пользует одну структуру данных — список узлов L. Во время работы алгоритма на ребрах графа будет ставиться метка, говорящая о том, что их уже проверили, это делается во избежание повторной проверки.

Алгоритм работает, осуществляя пять перечисленных ниже шагов.

1. Для каждого узла N в графе выполняются следующие пять шагов, где N явля­-
   ется начальным узлом.

1. Задаем начальные условия: L — пустой список, все ребра не маркированы.

1. Текущий узел добавляем в конец списка L и проверяем количество появле-­
   ний узла в списке. Если узел присутствует в двух местах, граф содержит
   цикл (записанный в список L) и работа алгоритма завершается.

2. Для заданного узла смотрим, выходит ли из него хотя бы одно немаркирован­-
   ное ребро. Если да, то переходим к шагу 5, если нет, то переходим к шагу 6.

3. Случайным образом выбираем любое немаркированное исходящее ребро и
   отмечаем его. Затем по нему переходим к новому текущему узлу и возвра­-
   щаемся к шагу 3.

4. Теперь мы зашли в тупик. Удаляем последний узел из списка и возвраща­-
   емся к предыдущему узлу, то есть тому, который был текущим перед тупи-­
   ковым узлом. Обозначаем его текущим узлом и возвращаемся к шагу 3. Если
   это первоначальный узел, граф не содержит циклов и алгоритм завершается.

Этот алгоритм по очереди берет каждый узел в качестве корня того, что, как он надеется, окажется деревом, и выполняет в дереве поиск в глубину. Если в про­цессе обхода алгоритм возвращается к уже встречавшемуся узлу, то он нашел цикл. Если алгоритм обходит все ребра из какого-нибудь заданного узла, то он возвраща­ется к предыдущему узлу. Если он возвращается к корню и не может идти дальше, то подграф текущего узла не содержит циклов. Если данное свойство сохраняется для всех узлов, значит, полный граф не содержит циклов, а система не заблокирована.

Чтобы увидеть, как работает описанный алгоритм на практике, воспользуемся графом на рис. 3.3, а. Порядок обработки узлов произвольный, поэтому будем ис­следовать их слева направо и сверху вниз. Тогда алгоритм начнет поиск с узла R, затем последовательно с узлов А, В, С, 5, D, T, E,F и т.д.. Если мы натолкнемся на цикл, алгоритм остановится.

Мы начинаем с узла R и инициализируем L как пустой список. Затем добавляем узел R в список, переходим к единственно возможному узлу А, и его также добавля­ем к списку L, получая L = [R, А]. Из узла А следуем к узлу 5, получая L = [R, A, S]. Узел 5 не имеет исходящих ребер, следовательно, это тупик, который заставляет нас вернуться к узлу А. Так как у узла А тоже нет немаркированных исходящих ребер, мы возвращаемся к узлу R, завершая, таким образом, его исследование.

Теперь снова начнем поиск, стартуя с узла А и предварительно вернув список L в исходное состояние. Эта часть алгоритма тоже быстро остановится, поэтому вы­полним процесс заново, начиная с узла В. Из узла В алгоритм будет следовать ис­ходящим ребрам до тех пор, пока не достигнет узла D; в это время список будет

таким: L = [В, Т, Е, V, G, U, D]. Теперь мы должны сделать (случайный) выбор. Если выбрать узел S, мы попадаем в тупик и возвращаемся к узлу D. Во второй раз выби­раем узел Т и получаем измененный список L = [В, Т, Е, V, G, U, D, Т\, в этот мо­мент мы обнаруживаем цикл и останавливаем алгоритм.

Этот алгоритм далек от оптимального. Тем не менее он демонстрирует существование алгоритма для обнаружения взаимо­блокировок.

Обнаружение взаимоблокировок при наличии нескольких ресурсов каждого типа

Когда в системе существует несколько экземпляров некоторых из ресурсов, для обнаружения взаимоблокировок необходим другой метод. Сейчас мы расскажем об основанном на матрицах алгоритме, обнаруживающем тупики среди п процессов, от Р₁, до Р_n. Пусть m — это число классов ресурсов, причем в системе E₁, ресурсов класса 1, Е₂ ресурсов класса 2 и, в общем, E ресурсов класса i (где 1 ≤ i ≤ т). Е — это вектор существующих ресурсов. Он передает общее количество имеющихся в наличии экземпляров каждого ресурса. Например, если класс 1 представляет со­бой накопители на магнитных лентах, то Е₁ = 2 означает, что в системе есть два магнитофона.

Существующие ресурсы Доступные ресурсы

( Е₁, Е₂, Е₃, Й, Е_м) (А₁, А₂, А₃, Й, А_м, )

Матрица текущего Матрица запроса

Распределения

С₁₁ С₁₂ С₁₃ …. С_1м R₁₁ R₁₂ R_{13 ……} R_1м

С₂₁ С₂₂ С₂₃ …. С_2м R₂₁ R₂₂ R_{23 ……} R_2м

. . . . . . . .

. . . . . . . .

Характеристики

Список файлов книги