Распределение и критерий хи-квадрат

3. Распределение и критерий хи-квадрат

Распределение Хи-квадрат (-распределение с  сте­пенями свободы), это распределение вероятностей, заданное плот­ностью вероятностей

                                     (*)

где  - гамма-функция. При  -распределение имеет моду в точке . Характеристическая функция -распределения имеет вид

,

математическое ожидание и дисперсия -распределения равны, соответ­ственно,  и . -распределение с  степенями свободы может быть выведено как распределение суммы квадратов   независимых случайных величин , имеющих стандарт­ное нормальное распределение с параметрами 0 и 1. Сумма неза­висимых случайных величин  с  степенями сво­боды, соответственно, подчиняется -распределению с  сте­пенями свободы.

Благодаря тесной связи с нормальным распределением -распределение играет важную роль в теории вероятностей и математичес­кой статистике. -распределение и многие другие распределения, кото­рые определяются посредством -распределения (например, Стьюдента распределение), описывают выборочные распределения различных функций от нормально распределённых результатов наблю­дений и используются для построения доверительных интерва­лов и статистических критериев. Так, например, для независи­мых случайных величин  с одинаковым нормальным распределением с математическим ожиданием  и дисперсией  отношение , где

, ,

подчиняется -распределению с  степенями свободы при любых значе­ниях  и . Этот результат положен в основу построения дове­рительных интервалов и критерия для проверки гипотезы о неизвестном значении  в случае, когда  также неизвестно. Особую известность в связи с -распределением получил -критерий, основанный на так называемой -статисти­ке Пирсона.

Рекомендуемые материалы

Имеются подробные таблицы -распределения, удобные для статисти­ческих расчётов. При больших объёмах выборок используют аппроксимацию посредством нормального распределения. При 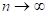 согласно центральной предельной теореме распределение нормированной величины ( стремится к стандартно­му нормальному распределению:

, ;

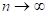более точная аппроксимация:

,

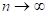
(здесь  - функция распределения стандартного нормального закона).

Впервые -распределение было рассмотрено немецким математиком Р. Хельмертом (1876) и английским математиком К. Пирсоном (1900).

Хи-квадрат критерий (-критерий) это критерий провер­ки различных статистических гипотез, основанный на -квад­рат распределении. Пусть, например, результаты наблюдений  являются взаимно независимыми случайными величи­нами, подчиняющимися одному и тому же нормальному распре­делению с неизвестными параметрами  и . Для проверки гипотезы , пользуются -критерием в следующей форме: если для заранее выбранных значений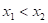

,

где

,

то полагают, что результаты наблюдений не противоречат гипо­тезе . Если же одно из этих неравенств нарушается, то считают расхождение значимым с уровнем значимости  и гипо­тезу  отклоняют. Пределы  и х₂ выбираются по задан­ному  на основании того, что при гипотезе  статистика

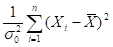
имеет распределение с  степенями свободы, т. е.  и х₂ находятся из уравнений

, .

Наиболее известно применение  критерия как критерия согласия Пирсона в следующей задаче. Пусть в серии п повторных неза­висимых испытаний с исходами  получен результат (), где  — случайное число осуществлении исхода  так, что . Проверяется гипотеза о том, что вектор () имеет полиномиальное распределение с соответствен­ными вероятностями  (, ; ).  критерий для этой гипотезы основан на статистике Пирсона

,

Обратите внимание на лекцию "9 Тепловой расчёт регенератора".

которая в пределе при 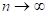 имеет  распределение с  степенями свободы. Согласно  критерию с уровнем значимос­ти, приближённо равным , гипотезу согласия отвергают, если , где  находится из соотношения

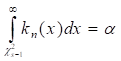
( - плотность  распределения с  степенями свободы). Та же статистика  используется для проверки ги­потезы о неизвестной функции распределения  независи­мых одинаково распределённых результатов наблюдений . Критерий для проверки гипотезы о том, что , где  — заданная функция распределения, строится следующим образом. Область значений каждой из величин  разбивается на конечное число  непересекающихся интервалов , , и вычисляются  - — число , ,  и  — веро­ятности  в предположешш, что проверяемая гипо­теза верна. Проверка гипотезы соответствия частот  вероят­ностям  основана на статистике

,

которая в случае, если , имеет асимптотическое рас­пределение  с  степенями свободы.

-критерий используется также как критерий однородности, кри­терий независимости в таблицах сопряжённости признаков и т. д.