§ 5. Доминирующие и полезные стратегии

Иногда применение некоторых из чистых стратегий нецелесообразно и при определении оптимальных смешанных стратегий их не следует учитывать. Те чистые стратегии, которые входят в состав оптимальной смешанной стратегии, называются полезными стратегиями.

Предположим, что для двух чистых стратегий δ_l и δ_k первого игрока имеет место следующее неравенство:

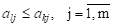
В этом случае нет смысла применять стратегию δ_k (т.к. для первого игрока это проигрыш и стратегия с наибольшим проигрышем должна быть отброшена) и δ_l – доминирующая стратегия по отношению к стратегии δ_k..

Аналогичным образом определяется стратегия второго игрока. Пусть для двух чистых стратегий второго игрока θ_l и θ_k имеет место неравенство:

Тогда θ_l – доминирующая стратегия второго игрока (для второго игрока это выигрыш и отбрасывается стратегия с наименьшим выигрышем).

 Предположим, что в рассматриваемой игре ни одна из стратегий не доминирует над другими. В этой ситуации пытаемся ответить на вопрос: все ли стратегии являются полезными, то есть входят в оптимальную смешанную стратегию?

Пусть у второго игрока имеется конечное число стратегий, то исходная игра сводится к так называемой S-игре. Попытаемся вывести понятие «S-игра».

Пусть имеется А = (а_ij), i = 1,…,n;  j = 1,…,m – матрица потерь первого игрока. Каждой стратегии δ_i первого игрока ставим в соответствие точку с_i = (a_i1, a_i2,…,a_im) в m-мерном пространстве, где координатами являются потери.

Рекомендуемые материалы

Игра, заданная множеством точек {с_­1,c₂,…,c_n} называется S-игрой.

Сначала первый игрок выбирает одну из точек с_i. Независимо от первого игрока второй выбирает координату точки, например а_i2, при этом говорят, что потери первого игрока составляют а_i2.

Если у второго игрока имеется две стратегии, то S-игра допускает наглядную интерпретацию. Предположим, что матрица игры выглядит следующим образом:

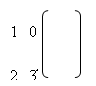S-игра: с₁ = (1,0);

      с₂ = (2,3);

      с₃ = (-1,1);

      с₄ = (0,-1);

      с₅ = (1,2).

Рис.1

Отмечаем точки на плоскости и соединяем их прямыми линиями для получения выпуклого множества (рис.1).

Если Вам понравилась эта лекция, то понравится и эта - 46 Зеркальные антенны.

S = l₁c₁+l₂c₂+l₃c₃+l₄c₄ , где

Теорема 1. Любая смешанная стратегия первого игрока может быть представлена точкой, принадлежащей выпуклой оболочке S* и наоборот.

Выпуклая оболочка S* конечного множества (с₁,…,с_n) является выпуклым многогранником в n-мерном пространстве. Точка S_o, являющаяся граничной, будет принадлежать обязательно одной из его граней, вершины которой и будут соответствовать полезной стратегии первого игрока. Учитывая, что число вершин любой грани не может превышать общего числа его вершин (то есть числа n ) и не может превышать размерности пространства (то есть числа m) приходим к выводу, что число полезных стратегий первого игрока не превышает  min{n,m}.

Теорема 2. Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш игроков остается неизменным и равным цене ã, независимо от того, какую смешанную стратегию применяет другой игрок, если только он не выходит за пределы своих полезных стратегий.

Доказательства этих теорем можно найти в [  ].