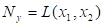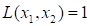Функциональное моделирование
ЛЕКЦИЯ 5
5.1. Функциональное моделирование
При проектировании РЭА необходимо исследовать процессы преобразования сигнала от входа к выходу. Такие процессы можно моделировать на ЭВМ достаточно точно на основе физического подхода методами схемотехнического моделирования. Однако это усложняет расчеты и требует много времени. Значительно быстрее можно выполнить моделирование на основе информационного подхода методами функционального моделирования (ФМ), которое является, безусловно, приближенным, однако, его точность вполне достаточна для решения задач на данном уровне проектирования.
Суть функционального моделирования заключается в разбиении РЭА на отдельные функциональные блоки, каждый из которых выполняет определенное функциональное преобразование сигнала (усиление, ограничение, интегрирование и т.д.). Под формой сигнала понимается либо зависимость сигнала от времени x(t) при моделировании во временной области, либо эквивалентное представление сигнала в виде изображения по Лапласу x(p) или зависимость от комплексной частоты jw при моделировании в частотной области. Основным требованием при функциональном моделировании является скорость, чтобы можно было исследовать как можно больше вариантов функциональных схем.
Приближенный характер функционального моделирования требует определенных допущений:
1) развязка – независимость работы отдельных блоков от других;
2) однонаправленность элементов – сигнал от входа распространяется на выход (нет влияния выходного блока на свой вход).
Так, например, требование развязки эквивалентно условию: Rвх = ∞, Rвых = 0 для каждого блока, а требование однонаправленности запрещает замыкать выход элементов в функциональной схеме.
Рекомендуемые материалы
5.2. Базовые элементы функциональных схем
Элементы функциональных схем можно свести к четырем базовым:
1) генераторы сигналов;
2) безынерционные элементы;
3) инерционные линейные элементы;
4) инерционные нелинейные элементы.
5.2.1. Генераторы сигналов
Различают две разновидности генераторов сигналов:
1) независимые, или задающие сигнал x(t) на входе функциональных схем;
2) управляемые, формирующие ту или иную форму сигнала x(t) в зависимости от управляющего воздействия U:
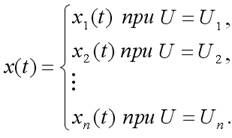

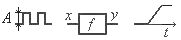
Рис. 5.1. Условное обозначение генератора сигналов:
независимый генератор (слева), управляемый генератор (справа)
5.2.2. Безынерционные элементы
Безынерционные элементы могут быть линейными и нелинейными и различаются соответственно линейной или нелинейной функцией преобразования y = f(x).
В отличие от линейного нелинейный элемент преобразует форму сигнала (ограничение, детектирование, формирование импульса другой формы и т.д.). Моделирование таких элементов проводится с целью построения временных диаграмм (без учета инерционности переходных процессов) и проверки правильности функционирования при изменении параметров сигнала и характеристик устройства в заданном диапазоне.

Рис. 5.2. Условное обозначение безынерционного элемента
Основные типы безынерционных элементов приведены в табл. 5.1.
5.2.3. Инерционные линейные элементы
Инерционные линейные элементы осуществляют преобразование во временной области в соответствии с выражением  , где h(t – τ) – переходная характеристика, а в частотной области – в соответствии с выражением y(p) = k(p)x(p), где k(p) – коэффициент передачи.
, где h(t – τ) – переходная характеристика, а в частотной области – в соответствии с выражением y(p) = k(p)x(p), где k(p) – коэффициент передачи.
К таким элементам относятся фильтры, линейные усилители, операционные усилители и т.п.
Таблица 5.1
Основные типы безынерционных элементов
Тип элемента | Выполняемое преобразование | Примечание |
| Аналого- аналоговый Аналого- импульсный Импульсно- аналоговый Аналого- цифровой Цифро- аналоговый Аналого- логический Логико- аналоговый Цифровой Логический Логико- цифровой Логико- импульсный |
|
импульсная модуляция
логической переменной
Импульсы на выходе при
|

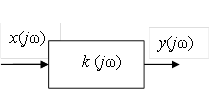
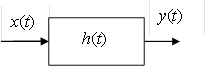
Рис. 5.3. Условные обозначения инерционных линейных элементов
5.2.4. Инерционные нелинейные элементы
В инерционных нелинейных элементах функцией преобразования является некоторый нелинейный оператор A(x), например, дифференциальное уравнение (ДУ), как наиболее универсальная форма представления, удобная для реализации на ЭВМ численными методами. Если порядок ДУ велик и построение модели затруднительно, то инерционный нелинейный элемент приближенно моделируют путем соединения инерционного линейного элемента и безынерционного нелинейного элемента, что описывается выражением у(t) = f [ ].
].


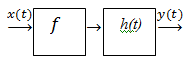
а б в
Рис. 5.4. Инерционный нелинейный элемент:
а – условное обозначение;
б, в – эквивалентное представление
Выходной сигнал и погрешность вычисления получаются разными при разном эквивалентном представлении. Так, ошибка численного вычисления интеграла в первой (б) эквивалентной схеме усиливается в нелинейном элементе. Однако точность моделирования определяется не только точностью вычисления, но и точностью моделирования в целом. Поэтому для приближенной оценки модель (б) может оказаться достаточной.
5.3. Моделирование базовых функциональных элементов
При моделировании функциональных элементов необходимо по заданному значению сигнала x вычислить его выходную величину у. Рассмотрим алгоритмы моделирования базовых функциональных элементов.
5.3.1. Безынерционные элементы
При моделировании элементов данного типа проблем не возникает, поскольку функция y = f (x) может быть вычислена в любой момент времени.
5.3.2. Генераторы сигналов
При моделировании непрерывная функция y = x(t) заменяется дискретной функцией хn = х (tn) в известные моменты времени tn . Для упрощения и ускорения вычислений используют рекуррентные формулы хn = f (xn – 1, xn – 2, …), где
xn – 1, xn – 2 – известные ранее вычисленные значения функции.
Примеры.
1. Моделируя y = x(t) = k eωt, можно использовать следующее рекуррентное соотношение: xn= xn–1k eωΔt . Таким образом, один раз вычислив eωΔt = A, все остальное находим по простой рекуррентной формуле:  ;
;  .
.
2. Моделируя сигналы y1 = x1(t) = sin ωt, y2 = x2(t) = cos ωt, можно представить sin ωtn = sin ω(tn–1 + Δt), cos ωtn = cos ω(tn–1 + Δt) и получить рекуррентные формулы: x1n = A1 x1, n – 1+ A2 x2, n – 1; x2n = A1 x2, n – 1+ A2 x1, n – 1, где A1 = cos ωΔt, A2 = sin ωΔt, x1,0 = 0, x2,0 = 1, причем x1n сигналы x1, n и x2, n моделируются попеременно.
5.3.3. Инерционные линейные элементы
Способы моделирования зависят от способа задания элемента, а именно: в частотной (задан коэффициент передачи) или временной (задана переходная характеристика) области.
Во временной области численное преобразование выполняется методом скользящего суммирования.
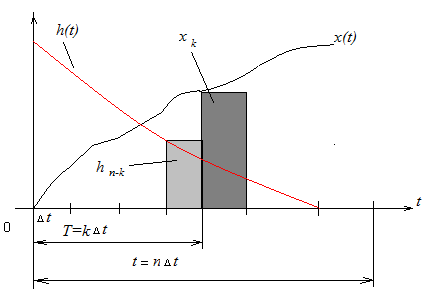
Рис. 5.5. Иллюстрация метода скользящего суммирования
Скользящее суммирование заключается в следующем:
1) заданный интервал интегрирования [0, t] и интервал текущего времени интегрирования [0, τ] разбивают на n отрезков ∆t, получая t = n∆t, τ = k∆t,
t – τ = (n – k) ∆t;
2) считая на каждом из отрезков ∆t значения x(t) и h(t – τ) постоянными (что соответствует численному интегрированию методом прямоугольников), получают при d τ ≈Δt вместо интеграла его дискретную аппроксимацию в виде суммы (дискретной свертки интеграла).
В частотной области используется представление входного, выходного сигналов и коэффициента передачи в виде комплексных чисел в алгебраической или показательной форме.
5.3.4. Инерционные нелинейные элементы
Если инерционный нелинейный элемент задан обыкновенным дифференциальным уравнением (ОДУ), то он моделируется во временной области путем дискретизации и алгебраизации ОДУ.
Дискретизация состоит в замене производных конечно-разностным аналогом. В результате дискретизации ОДУ превращается в алгебраическое уравнение относительно уn + 1 и решается численными методами. Такой же подход справедлив для элементов, описываемых ДУ и более высоких порядков (в частных производных).
5.4. Моделирование элементов во временной области,
заданных коэффициентом передачи
Имеем непрерывный входной сигнал x(t). При моделировании на ЭВМ непрерывный сигнал заменяется дискретным xn = x(tn), взятым в момент времени tn. В промежутках tn<t<tn+1 значение сигнала не определено. Его можно, например, считать постоянным и равным xn. В этом случае можно считать, что на вход элемента поступает последовательность скачков, а выходной сигнал является суммарным откликом на эти скачки.
При моделировании переходят от непрерывного входного сигнала x(t) и коэффициента передачи k(p) к эквивалентному дискретному элементу k’(p) и дискретному сигналу xn. Известен ряд математических способов такого перехода на основе рекуррентных формул.
Контрольные вопросы к лекции
1. Какой подход лежит в основе функционального моделирования?
2. Какие допущения предполагает функциональное моделирование?
3. Перечислить базовые элементы функциональных схем.
4. Каковы основные свойства безынерционных элементов?
Вместе с этой лекцией читают "5 Связь педагогики с другими науками".
5. Каковы основные свойства инерционных линейных элементов?
6. Каковы основные свойства инерционных нелинейных элементов и как их учитывают при моделировании?
7. Как моделируют безынерционные элементы?
8. Как моделируют генераторы сигналов?
9. Как моделируют инерционные линейные элементы?
10. Как моделируют инерционные нелинейные элементы?


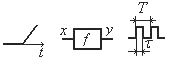
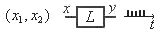
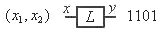
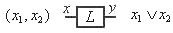

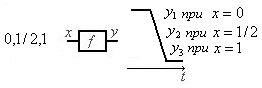
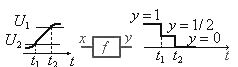
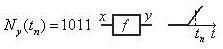
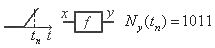
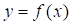
 – широтно-
– широтно-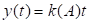
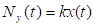
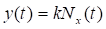
 ,
,  ,
, – значения
– значения  – электрические уровни,
– электрические уровни,  – форма сигнала
– форма сигнала 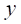
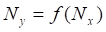
 ,
,  – логическая функция
– логическая функция