Аэродинамические характеристики самолета при неустановившемся движении
Лекция 22
Тема 8: Аэродинамические характеристики самолета при неустановившемся движении
8.1. Кинематические параметры, аэродинамические силы и моменты при неустановившемся движении
8.1.1. Понятие о неустановившемся движении. Кинематические параметры
Определение: неустановившимся движением (нестационарным) называется движение самолета, при котором хотя бы в одной точке его поверхности параметры потока изменяются с течением времени.
В общем случае неустановившееся движение определяется скоростью
движением центра масс, которое описывается скоростью движения V(t) углом атаки  (t) и углом скольжения
(t) и углом скольжения  (t),движением вокруг центра масс, описываемым угловым скоростями вращения вокруг соответствующих осей координат
(t),движением вокруг центра масс, описываемым угловым скоростями вращения вокруг соответствующих осей координат  (t),
(t), (t) и
(t) и (t).Эти шесть параметров, описывающих движение летательного аппарата как твердого тела, называются кинематическими параметрами движения .
(t).Эти шесть параметров, описывающих движение летательного аппарата как твердого тела, называются кинематическими параметрами движения .
Кроме того ,к кинематическим параметрам относятся параметры деформации ЛА- и параметры ,характеризующие турбулентность атмосферы вдоль осей координат -
и параметры ,характеризующие турбулентность атмосферы вдоль осей координат - (x,y,z,t),
(x,y,z,t),  (x,y,z,t),
(x,y,z,t),  (x,y,z,t) которые являются функциями не только времени ,но и координат.
(x,y,z,t) которые являются функциями не только времени ,но и координат.
Рекомендуемые материалы
При исследовании аэродинамических характеристик удобно пользоваться указанными параметрами в безразмерном виде :
u= ,
,
 =
= ,
, 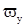 =
= ,
, 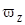 =
= ,
,  ,
,  ,
,  ,
,
b=b - для
- для 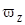 , b=
, b= -для
-для 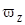 ,
,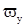
V -средняя скорость неустановившегося движения ,
-средняя скорость неустановившегося движения ,
b-линейный размер (b=b -в продольном движении,b=
-в продольном движении,b= -в боковом движении.)
-в боковом движении.)
Для сокращения записи иногда используются обозначения кинематических параметров через qi.Например , q1= , q2=
, q2= , q3=
, q3= и т .д.
и т .д.
При определении нестационарных аэродинамических характеристик задача может решаться отдельно для каждого параметра .В этом случае говорят, что решается qi-задача (например , -задача ,
-задача ,  -задача и т.д.).
-задача и т.д.).
В ряде случаев неоходимо знание производных кинематических параметров по времени :
 , ,
, , 
 ,
, =
= ,
, =
= ,
, =
= ,
, ,
, ,
,
 ,
, где
где  - безразмерное время.
- безразмерное время.
Эти производные получили название «qi » с точкой ( i). Иногда их также называют кинематическими параметрами.
i). Иногда их также называют кинематическими параметрами.
8.1.2. Аэродинамические силы и моменты при неустановившемся движении
При нестационарном движении результирующую аэродинамическую силу и ее момент можно записать в виде:
R (t)=c
(t)=c (t)
(t)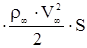 ,
,
M (t)=m (t)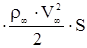
 ,
,
Коэффициенты c (t), m (t) при неустановившемся движении являются функциями времени и кинематических параметров qi, которые в свою очередь зависят от времени. Поэтому: c
(t), m (t) при неустановившемся движении являются функциями времени и кинематических параметров qi, которые в свою очередь зависят от времени. Поэтому: c = c
= c (qi)= c
(qi)= c (u,
(u, …), m=m(qi)= =m(u,
…), m=m(qi)= =m(u, …).В линейных задачах эти выражения можно записать в виде :
…).В линейных задачах эти выражения можно записать в виде :
c = c
= c + c
+ c + c
+ c + c
+ c + c
+ c +. . .,
+. . .,
m = m
= m + m
+ m + m
+ m + m
+ m + m
+ m +. . .,
+. . .,
В данном выражении каждый член суммы представляет собой коэффициент
c или m
или m , полученный при решении частной задачи и не зависящий от других параметров. Индекс “0” означает, что c
, полученный при решении частной задачи и не зависящий от других параметров. Индекс “0” означает, что c и m
и m получены для начального рассматриваемого момента движения. При анализе неустановившегося движения общее движение разделяют на продольное и боковое .
получены для начального рассматриваемого момента движения. При анализе неустановившегося движения общее движение разделяют на продольное и боковое .
Продольное движение определяется параметрами :  .
.
Боковое движение определяется параметрами:  ,
, ,
,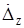
Параметры  ,
, ,
, ,
, ,
, ,
, являются общими .
являются общими .
В продольном движении различают два частных случая: поступательное возмущенное движение относительно O и колебательное движение относительно оси O
и колебательное движение относительно оси O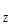 .
.
Поступательное возмущенное движение вдоль оси O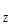
Примером такого движения может быть вход в вертикальный порыв .При входе в
вертикальный порыв скорость V изменяется по величине и по знаку .Кроме изменения
изменяется по величине и по знаку .Кроме изменения  изменяется величина производной
изменяется величина производной  , и следовательно, параметр
, и следовательно, параметр
 . При этом изменяются
. При этом изменяются  и
и  , но настолько незначительно, что их влиянием на нестационарные силы и моменты пренебрегают .
, но настолько незначительно, что их влиянием на нестационарные силы и моменты пренебрегают .
Поэтому :
c =c
=c +c
+c + c
+ c ,
,
m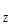 =m
=m +m
+m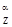
 + m
+ m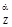
 .
.
где c и m
и m -характеристики ,соответствующие началу возмущенного движения
-характеристики ,соответствующие началу возмущенного движения
Колебательное движение относительно оси О с угловой скоростью
с угловой скоростью  (t)
(t)
 |
Изменение угла атаки
 по времени характеризуется производной
по времени характеризуется производной  .Так
.Так Рис.8.1
как
 является функцией времени ,то будет иметь место производная
является функцией времени ,то будет иметь место производная  .
.
Таким образом ,такое движение характеризуется кинематическими параметрами
 ,
,  ,
, . Поэтому c
. Поэтому c и m
и m в продольном движении определяются выражениями .
в продольном движении определяются выражениями .
c =c
=c +c
+c + c
+ c + c
+ c + c
+ c ,
,
m =m
=m +m
+m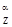
 + m
+ m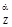
 + m
+ m + m
+ m .
.
Замечание: в продольном движении скорость изменения угла атаки по времени

 =
= =
=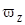
c = c
= c +C
+C +( c
+( c + c
+ c )
) ,
,
m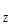 =m
=m +m
+m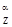
 +( m
+( m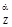 + m
+ m )
) + m
+ m ,
,
Обычно последними членами в данном выражении пренебрегают, так как они незначительны по сравнению с другими членами.
8.2. Демпфирующие моменты летательного аппарата
8.2.1. Характеристики продольного демпфирования
В предыдущей теме было установлено, что при  < 0 ЛА статически устойчив. Однако, процесс возвращения его к исходному режиму носит колебательный характер, т.е. зависит от времени t. Если колебания затухающие, то ЛА устойчив не только статически, но и динамически. Установлено, что если сумма (m
< 0 ЛА статически устойчив. Однако, процесс возвращения его к исходному режиму носит колебательный характер, т.е. зависит от времени t. Если колебания затухающие, то ЛА устойчив не только статически, но и динамически. Установлено, что если сумма (m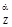 + + m
+ + m )<0, то колебания ЛА затухающие.
)<0, то колебания ЛА затухающие.
Вывод: для того, чтобы ЛА был динамически устойчив в продольном движении, необходимо выполнять условие (m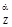 + m
+ m )<0, при этом коэффициенты m
)<0, при этом коэффициенты m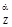 и m
и m называют коэффициентами продольного демпфирующего момента.
называют коэффициентами продольного демпфирующего момента.
Коэффициент m продольного демпфирующего момента ЛА
продольного демпфирующего момента ЛА
Продольный демпфирующий момент создается в основном горизонтальным оперением
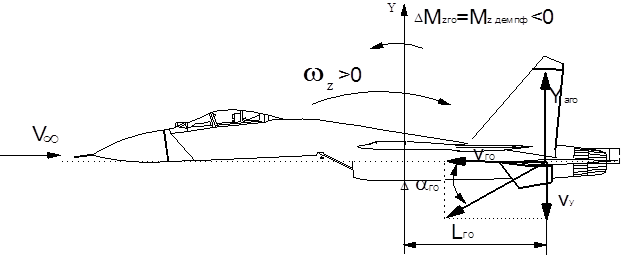 |
Рис.8.2
При вращении с угловой скоростью z горизонтальное оперение приобретает дополнительную скорость V =
z горизонтальное оперение приобретает дополнительную скорость V =  z L го и приращение угла атаки
z L го и приращение угла атаки
Daго= =
=
 ,
,
В результате на горизонтальном оперении появляется сила
DYaго= Daго
Daго ,
,
которая вызовет момент
DMZго= - DYaгоLго
- DYaгоLго
Коэффициент демпфирующего момента m после соответствующих преобразований получается в виде
после соответствующих преобразований получается в виде
m = -
= -  KvAго
KvAго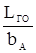
где Aго= - статический момент оперения.
- статический момент оперения.
Замечание: чем больше Аго , тем лучше демпфирующие характеристики летательного аппарата.
Коэффициент m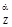 продольного демпфирующего момента летательного аппарата
продольного демпфирующего момента летательного аппарата
Допустим, что угол атаки крыла a увеличивается по времени со скоростью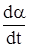
Известно, что скос потока от крыла уменьшает угол атаки горизонтального оперения на величину e. Поэтому с увеличением a скос e будет увеличиваться, но с запаздыванием, и в силу этого по сравнению с установившимся движением на данном a на оперении появляется сила DYaго , которая относительно центра масс ЛА вызовет момент, уменьшающий a
Вывод: в общем виде момент демпфирования тангажа определяется выражением
MZдепфир= (m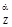 + m
+ m )
) qSbA
qSbA
8.2.2. Характеристики бокового демпфирования
Известно, что боковая статическая устойчивость характеризуется условиями:
m < 0 - ЛА устойчив в поперечном движении,
< 0 - ЛА устойчив в поперечном движении,
m < 0 - ЛА устойчив в путевом отношении.
< 0 - ЛА устойчив в путевом отношении.
Поперечный и путевой демпфирующие моменты характеризуются производными m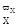 и m
и m + m
+ m .
.
Демпфирующий момент крена
Поперечный демпфирующий момент создается в основном крылом. При вращении ЛА относительно оси ОХ с угловой скоростью  x во всех сечениях крыла возникает дополнительная окружная скорость Vy=
x во всех сечениях крыла возникает дополнительная окружная скорость Vy= x z , что приводит к увеличению углов атаки на Da=
x z , что приводит к увеличению углов атаки на Da= и появлению прироста нормальной силы DY , которая вызовет демпфирующий момент
и появлению прироста нормальной силы DY , которая вызовет демпфирующий момент
MZдемпф= m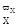
 qSl
qSl
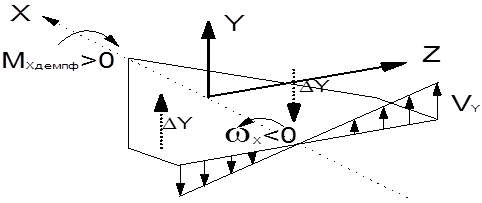 |
Рис.8.3
Определенную долю в величину этого момента вносит и боковая сила, возникающая на ВО.
m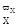 <0 - ЛА динамически устойчив по крену
<0 - ЛА динамически устойчив по крену
Демпфирующий момент рыскания
Информация в лекции "3.7 Источники и литература" поможет Вам.
Природа возникновения путевого демпфирующего момента аналогична природе возникновения продольного демпфирующего момента, лишь роль горизонтального оперения в данном случае играет вертикальное оперение
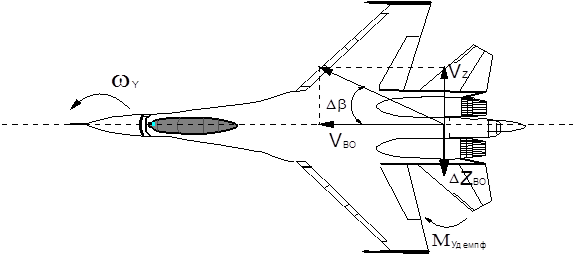 |
Рис.8.4
Величина путевого демпфирующего момента определяется выражением
MYдепф = (m + m
+ m )vyqSl
)vyqSl
(m + m
+ m ) <0 - ЛА динамически устойчив в путевом отношении.
) <0 - ЛА динамически устойчив в путевом отношении.






















