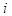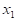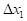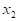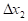Численное решение систем нелинейных уравнений
Численное решение систем нелинейных уравнений
Постановка задачи
Дана система линейных уравнений
 (1)
(1)
Введём обозначения: вектор  - вектор аргументов:
- вектор аргументов:
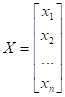
Аналогично вектор функций
Рекомендуемые материалы
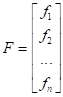
Тогда систему 1 можно переписать в виде:
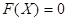
Система линейных уравнений в общем виде неразрешима. Поэтому мы будем рассматривать только численные методы решения системы линейных уравнений.
Метод Ньютона
Для уравнения имеет вид:
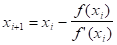
По анологии метод Ньютона для системы линейных уравнений
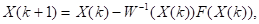
где 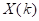 - вектор аргументов на
- вектор аргументов на  -ом шаге итерации
-ом шаге итерации
 - значения вектора функций (системы уравнений ) при
- значения вектора функций (системы уравнений ) при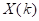
 - обратная матрица Якоби
- обратная матрица Якоби
 - матрица, Якоби-матрица, состоящая из частных производных
- матрица, Якоби-матрица, состоящая из частных производных
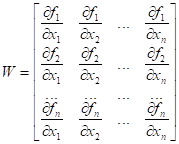
Вполне естественно очевидно, что формулу Ньютона можно применять в том случае, когда Якоби-матрица неособенная, невырождённая, то есть  .
.
Пример:
Дано: 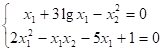
Матрица Якоби
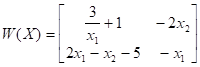
Превоначальная оцнка
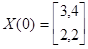
1) 
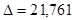
2) 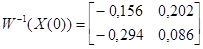
3) 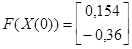
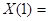
 -
-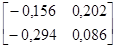
 =
= -
- =
=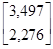
и так далее
Результаты итераций лучше всего сводить в таблицу
|
|
|
|
|
|
| 0 | 3,4 | 0,097 | 2,2 | 0,076 |
| 1 | 3,497 | 2,276 | ||
| 2 |
Прекращаем вычисления, когда  - заданная точность.
- заданная точность.
Как и в любых численных методах встают следующие задачи: о сходимости метода и о выборе начального значения.
Сходимость метода Ньютона
Вопросами сходимости метода Ньютона занимались такие учёные, как Виллус, Стёпин, Островский, Канторович и другие. Мы же будем рассматривать сходимость, единственность корня и выбор начального условия по Канторовичу. При рассмотрении этих характеристик метода ипользуются понятия нормы. Поэтому прежде дадим определения :
 -нормой - называется максимальная сумма модулей элементов по строкам.
-нормой - называется максимальная сумма модулей элементов по строкам.
 -нормой - называется максимальная сумма модулей элементов по столбцам.
-нормой - называется максимальная сумма модулей элементов по столбцам.
 -нормой - нызывается квадратный корень из суммы квадратов модулей элементов матрицы
-нормой - нызывается квадратный корень из суммы квадратов модулей элементов матрицы
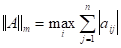
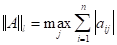
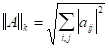
Пример:
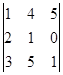
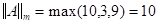
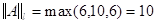
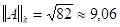
Для оценки матриц, используемых в методе Ньютона для нелинейных систем, будем использовать  -нормы, а именно
-нормы, а именно
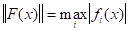
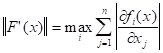
Теорема о существовании корней и сходимости процесса Ньютона
Пусть дана нелинейная система уравнений
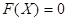 ,
,
где  - вектор-функция определена и непрерывна вместе со своими частными производными первого и второго порядков в некоторой области
- вектор-функция определена и непрерывна вместе со своими частными производными первого и второго порядков в некоторой области  . Положим, что
. Положим, что  - есть точка, лежащая в
- есть точка, лежащая в  вместе со своей замкнутой
вместе со своей замкнутой  -окрестностью. При этом выполняются следующие условия:
-окрестностью. При этом выполняются следующие условия:
1) матрица Якоби при  имеет обратную функцию
имеет обратную функцию

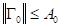
2) 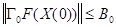
3) 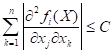
4) постоянные  удовлетворяют неравенству
удовлетворяют неравенству
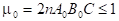
Тогда процесс Ньютона при начальном приблежении  сходится к решению
сходится к решению  - есть решение такое, что
- есть решение такое, что 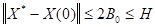
Для проверки условия  даёт оценку расходимости начального и первого приблежения.
даёт оценку расходимости начального и первого приблежения.
Быстрота сходимости процесса Ньютона
Если выполнимы все четыре условия теоремы 1, то для последовательных приближений 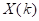 ,
,  справедливо неравенство:
справедливо неравенство:
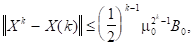
где  - искомое решение, а
- искомое решение, а 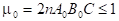
При  сходимость метода - сверхбыстрая.
сходимость метода - сверхбыстрая.
Единственность решения
Если выполнимы все четыре условия, в области
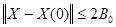
то содержится единственное решение системы
Выбор начального условия
Если выполнимы все четыре условия и  , то процесс сходится к единственному решению
, то процесс сходится к единственному решению  в основной области
в основной области 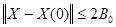 при любом выборе начального условия из области
при любом выборе начального условия из области
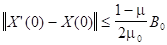
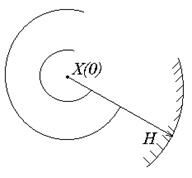
Модифицированный метод Ньютона
При использовании метода Ньютона наиболее трудоёмким является процесс вычисления обратной матрицы Якоби.
Если матрица  невырождённая для некоторого приближения
невырождённая для некоторого приближения  , и
, и  достаточно близко к
достаточно близко к  (искомому решению), то можно использовать модифицированный метод Ньютона.
(искомому решению), то можно использовать модифицированный метод Ньютона.
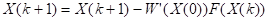
Метод итераций
Дана система нелинейных уравнений:
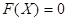
или
 (1)
(1)
Допустим, что систему 1 можно привести к виду:
 (2)
(2)
Введём обозначения:
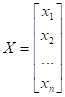 ,
,  ,
,
Можно систему уравнений 2 переписать в виде:
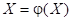
Приведённое матричное уравнение и есть формула метода итераций
Необходимое и достаточное условие сходимости процесса итерации
Пусть функции  и
и  непрерывны в области
непрерывны в области  , причём в области
, причём в области  выполнимо неравенство:
выполнимо неравенство:
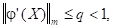
где  - некоторая константа.
- некоторая константа.
Если последовательные приближения
 ,
, 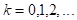
не выходят из области  , то этот процесс сходится к единственному решению системы.
, то этот процесс сходится к единственному решению системы.
Следствие:
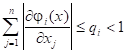
оценка пиближённо
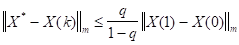
На практике лучше всего рассматривать матрицу с элементами
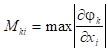
Для сходимости должно выполнятся условие
1) 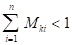
2) 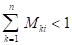
3) 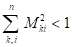
Метод скорейшего спуска (градиентный метод)
Дана система линейных уравнений:
 (1)
(1)
В матричном виде
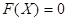
Считаем, что  действительны и непрерывно дифференцируемы в их общей области определения.
действительны и непрерывно дифференцируемы в их общей области определения.
Рассмотрим функцию
 (2)
(2)
Очевидно, что если мы найдём решение системы уравнений 1  , то это решение является и решением системы уравнений 2 и наоборот.
, то это решение является и решением системы уравнений 2 и наоборот.
Предполагаем, что система 1 имеет лишь одно изолированное решение, представляющего собой точку строго минимум функции  . Таким образом задача сводится к нахождению минимум функции
. Таким образом задача сводится к нахождению минимум функции  в
в  -мерном пространстве.
-мерном пространстве.
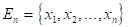
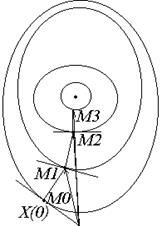
Берём точку  - нулевое приближение. Через точку
- нулевое приближение. Через точку  проходит поверхность уровня и
проходит поверхность уровня и  . Если
. Если  близка
близка  , то поверхность
, то поверхность  =
= будет похожа на элипсоид.
будет похожа на элипсоид.
Из точки  движемся по нормали к поверхности
движемся по нормали к поверхности  до тех пор, пока эта нормаль не коснётся
до тех пор, пока эта нормаль не коснётся  другой поверхности:
другой поверхности:
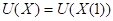
И так далее.
Так как  , то двигаясь таким образом, мы быстро приближаемся к точке с минимальным значением
, то двигаясь таким образом, мы быстро приближаемся к точке с минимальным значением  , которая соответствует некоему корню
, которая соответствует некоему корню  .
.
Градиент функции U
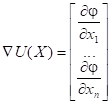
 - набла или grad - есть вектор приложенный к точке
- набла или grad - есть вектор приложенный к точке  , имеющий направление нормали. Из векторных произведений
, имеющий направление нормали. Из векторных произведений
 ,
,  (3)
(3)
Как определить  ? Для этого рассматривают скалярную функцию
? Для этого рассматривают скалярную функцию  :
:
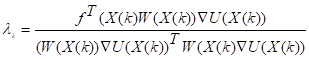
Уравнение 3 можно преобразовать так, чтобы не было явного выражения градиента. Введем обозначения  , тогда итерационная формула градиентного метода будет иметь вид:
, тогда итерационная формула градиентного метода будет иметь вид:
 ,
,
где 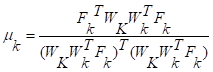
Вычисления производятся до тех пор, пока не станет справедливым следующее неравенство:
 e,
e,
где e - заданная точность вычисления.
Пример. Дана система нелинейных уравнений:
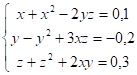
Найти решение системы градиентным методом с точностью e=0,01
Определим начальное приближение как:
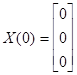
Вектор-функция  имеет вид:
имеет вид:
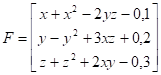
Якобиан, или матрица частных производных имеет вид:
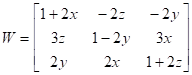
1 итерация
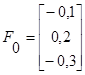
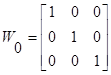
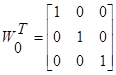
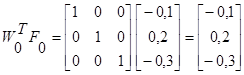
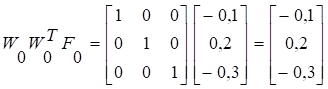
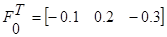
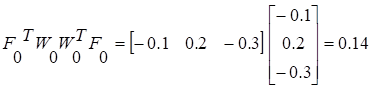
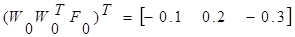
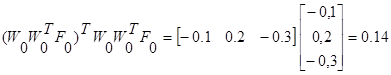
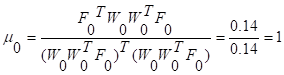
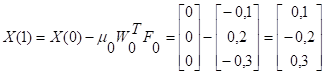
2 итерация
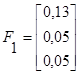
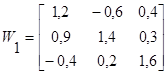
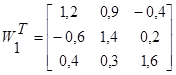
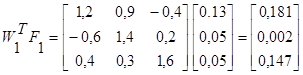
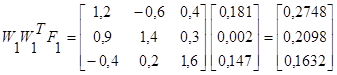
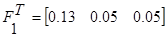
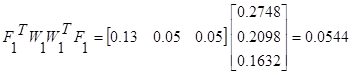
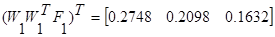
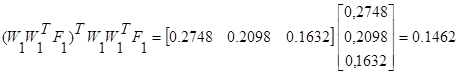
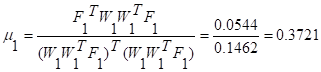
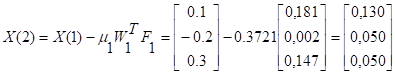
Решение системы нелинейных уравнений представлено в таблице:
| K | x | ½Dx½ | y | ½Dy½ | z | ½Dz½ |
| 0 | 0.000 | 0,100 | 0.000 | 0,200 | 0.000 | 0,300 |
| 1 | 0.100 | 0,030 | -0.200 | 0,250 | 0.300 | 0,250 |
| 2 | 0,130 | 0,095 | 0,050 | 0,251 | 0,050 | 0,209 |
| 3 | 0,035 | 0,018 | -0,201 | 0,016 | 0,259 | 0,013 |
| 4 | 0,017 | 0,003 | -0,185 | 0,007 | 0,246 | 0,001 |
| 5 | 0,014 | -0,178 | 0,245 |
Вместе с этой лекцией читают "Экскурсия и ее сущность".
Таким образом, решение системы уравнений имеет вид:
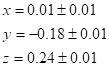
Сходимость градиентного метода
Сходимость метода гарантируется при выборе начального приближения вблизи  .
.
В любом случае метод может остановитья в точке относительного метода.