ДЗ 10: Линейная алгебра (Кузнецов Л.А.) вариант 27
Описание
Полный вариант все 12 задач:
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №1, вариант 27
Образует ли линейное пространство заданное множество, в котором определены сумма любых двух элементов a и b линейная алгебра и произведение любого элемента a на любое число α:
Условие варианта смотрите в задачнике.Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №2, вариант 27
Исследовать на линейную зависимость систему векторов:
Условие варианта смотрите в задачнике.Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №3, вариант 27
Найти общее решение для каждой из данных систем и проанализировать его структуру (указать базис пространства решений системы однородной системы, установить размерность пространства, выделить частное решение неоднородной системы).
В прошлом издании условие выглядит так: Найти какой-нибудь базис и определить размерность линейного пространства решений. Но система осталась без изменений:
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №4, вариант 27
Найти координаты вектора X в базисе (e'1, e'2, e'3), если он задан в базисе (e1, e2, e3):
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №5, вариант 27
Пусть x = (x1, x2, x3). Являются ли линейными следующие преобразования:
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №6, вариант 27
Пусть x = {x1, x2, x3}, Ax = {x2 - x3, x1, x1 + x3}:
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №7, вариант 27
Найти матрицу в базисе (e'1, e'2, e'3), где e'1 = e1 - e2 + e3, e'2 = e1 + e2 - 2e3, e'3 = -e1 + 2e2 + e3, если она задана в базисе (e1, e2, e3):
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №8, вариант 27
Доказать линейность, найти матрицу, область значений и ядро оператора:
Условие варианта смотрите в задачнике.Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №9, вариант 27
Найти собственные значения и собственные векторы матрицы:
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №10, вариант 27
Привести квадратичную форму к каноническому виду методом Лагранжа:
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №11, вариант 27
Привести квадратичную форму к каноническому виду ортогональным преобразованием:
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №12, вариант 27
Исследовать кривую второго порядка и построить ее:
![]()
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №1, вариант 27
Образует ли линейное пространство заданное множество, в котором определены сумма любых двух элементов a и b линейная алгебра и произведение любого элемента a на любое число α:
Условие варианта смотрите в задачнике.Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №2, вариант 27
Исследовать на линейную зависимость систему векторов:
Условие варианта смотрите в задачнике.Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №3, вариант 27
Найти общее решение для каждой из данных систем и проанализировать его структуру (указать базис пространства решений системы однородной системы, установить размерность пространства, выделить частное решение неоднородной системы).
В прошлом издании условие выглядит так: Найти какой-нибудь базис и определить размерность линейного пространства решений. Но система осталась без изменений:
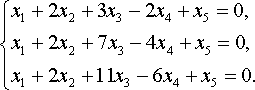
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №4, вариант 27
Найти координаты вектора X в базисе (e'1, e'2, e'3), если он задан в базисе (e1, e2, e3):
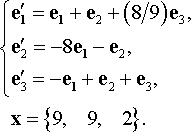
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №5, вариант 27
Пусть x = (x1, x2, x3). Являются ли линейными следующие преобразования:

Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №6, вариант 27
Пусть x = {x1, x2, x3}, Ax = {x2 - x3, x1, x1 + x3}:
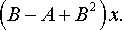
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №7, вариант 27
Найти матрицу в базисе (e'1, e'2, e'3), где e'1 = e1 - e2 + e3, e'2 = e1 + e2 - 2e3, e'3 = -e1 + 2e2 + e3, если она задана в базисе (e1, e2, e3):

Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №8, вариант 27
Доказать линейность, найти матрицу, область значений и ядро оператора:
Условие варианта смотрите в задачнике.Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №9, вариант 27
Найти собственные значения и собственные векторы матрицы:
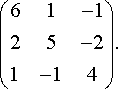
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №10, вариант 27
Привести квадратичную форму к каноническому виду методом Лагранжа:
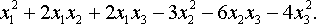
Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №11, вариант 27
Привести квадратичную форму к каноническому виду ортогональным преобразованием:

Линейная алгебра из задачника Л.А. Кузнецова 2005 года, задача №12, вариант 27
Исследовать кривую второго порядка и построить ее:

Характеристики домашнего задания
Предмет
Номер задания
Вариант
Теги
Просмотров
7
Качество
Идеальное компьютерное
Размер
2,33 Mb
Список файлов
X-01-27.jpg
X-02-27.jpg
X-03-27.jpg
X-04-27.jpg
X-05-27.jpg
X-06-27.jpg
X-07-27.jpg
X-08-27.jpg
X-09-27.jpg
X-10-27.jpg
X-11-27.jpg
X-12-27.jpg
Комментарии
Нет комментариев
Стань первым, кто что-нибудь напишет!
 dmitry0376
dmitry0376




















